I. Introducción

En nuestra cultura jurídica se requiere, como condición de buen ejercicio de la función de administrar justicia, que las decisiones de los jueces sean fundadas en derecho. Este requisito suele expresarse diciendo que la decisión debe constituir una "derivación razonada del derecho vigente". La ausencia de tal cualidad puede determinar que la sentencia sea declarada nula por carecer de un elemento esencial para que pueda ser reconocida como acto jurisdiccional.

Sin embargo, si bien parece claro que la exigencia de fundamentación no es satisfecha a menos que la sentencia contenga alguna argumentación que vincule el contenido de la decisión con lo que el juez —o la comunidad jurídica— identifica como derecho vigente, la determinación de los requisitos formales que ha de cumplir la argumentación resulta problemática.

En este trabajo discuto una interpretación muy difundida del concepto de fundamentación, a la que denomino "concepción deductivista", cuyos representantes más conspicuos son los profesores Carlos Alchourrón y Eugenio Bulygin. Su tesis central consiste en sostener que para cumplir con esa exigencia es necesario que el contenido de la decisión judicial sea consecuencia deductiva de ciertas premisas normativas —normas jurídicas generales— y fácticas —enunciados descriptivos—.

Sostengo que la defensa de la concepción deductivista necesita basarse en un análisis de la estructura lógica de las normas generales que es inadecuado. Asimismo, trato de mostrar que el razonamiento práctico por el cual se justifican decisiones mediante la invocación de normas no es de naturaleza deductiva.

El artículo se divide en seis secciones, incluyendo la presente. En la sección II presento la concepción deductivista, expongo algunas posibles objeciones que considero erróneas y la forma en que pueden ser refutadas por los defensores de dicha concepción. En la sección III caracterizo el sistema standard de lógica deóntica, muestro cómo puede ser obtenido a partir de la lógica modal y presento una semántica adecuada para ese sistema. Sobre la base de la semántica propuesta efectúo una distinción conceptual entre la inconsistencia normativa y la imposibilidad fáctica de cumplir con una norma o un conjunto de normas, y muestro algunas consecuencias absurdas que se siguen de ciertas formas de derivación de consecuencias normativas a partir de la combinación de premisas normativas y descriptivas. Finalmente, presento dos concepciones de las normas condicionales, las llamadas 'concepción puente' y 'concepción insular'. En la sección IV formulo tres objeciones a la concepción puente. La primera se refiere a la falta de transparencia del lenguaje lógico que tal concepción acarrea. La segunda, a la incompatibilidad de las dos concepciones, las dificultades que se presentan al tratar de combinarlas y la pérdida de capacidad expresiva que acarrearía el abandono de la concepción insular. La tercera, a algunas consecuencias antiintuitivas que se producen al combinar la concepción puente con la ley de refuerzo del antecedente de la lógica proposicional. En la sección V discuto la concepción del razonamiento práctico en que se basa la concepción puente. Argumento contra la idea de que la concepción insular carece de consecuencias prácticas y muestro que la tesis de que la justificación de acciones sobre la base de reglas es de naturaleza deductiva no podría sostenerse irrestrictamente, para todo tipo de reglas, sin caer en un regreso al infinito. La sección VI está destinada a la presentación de conclusiones.

II. Caracterización de la concepción deductivista de las sentencias

El requisito de que las sentencias judiciales sean fundadas expresamente en el derecho vigente ha sido vinculado con ciertos ideales políticos relativos a la función que corresponde a los jueces, los cuales se enmarcan en la doctrina política de la separación de poderes, en cuanto esta doctrina requiere que la función de los jueces se circunscriba a resolver los casos particulares de acuerdo con las reglas generales sancionadas por el poder legislativo.

Entre las razones que se puede invocar para justificar ese tipo de separación, Alchourrón(1996 a) identifica las siguientes:

a) El argumento de la igualdad formal: "cuando los jueces se limitan a aplicar las reglas generales promulgadas por el congreso, todos los casos del mismo tipo recibirán la misma solución".

b) El de la democracia: "en aquellos países en los que los miembros del congreso son elegidos democráticamente, lo cual usualmente no ocurre con los miembros de la judicatura, una separación tajante permite el control democrático del modo de resolver los desacuerdos entre los miembros de la comunidad".

c) El de la certeza y seguridad: "sólo por medio de una estricta división de poderes la gente está en condiciones de conocer sus derechos y obligaciones por anticipado respecto de las decisiones judiciales. Toda decisión que no sea justificada tal como se exige es considerada arbitraria, en el sentido de que los derechos u obligaciones adjudicados han sido establecidos ex post facto por el juez".

En la misma obra, Alchourrón denomina 'concepción del Sistema Maestro' a la concepción jurídica que surge del modelo ideal según el cual las decisiones de los casos particulares serán tomadas en concordancia con un conjunto de reglas generales previamente determinado y públicamente conocido. La caracteriza mediante tres principios, que denomina, respectivamente, 'de inexcusabilidad', 'de justificación' y 'de legalidad', los cuales son luego resumidos en la siguiente formulación: "los jueces deben resolver todos los casos que se les someten a juzgamiento dentro del límite de su competencia mediante decisiones fundadas en normas jurídicas del sistema".

La posibilidad de satisfacer esa exigencia, dice el autor, depende de la verdad de la siguiente afirmación, que denomina 'postulado de completitud': "en todo sistema jurídico hay normas que proveen fundamentos para resolver todo caso posible", para aclarar inmediatamente que "la verdad o falsedad del postulado depende principalmente de (i) cómo se interprete la noción de justificación y (ii) cómo se identifiquen los elementos del sistema jurídico".

Mi interés se centrará exclusivamente en el punto (i).

Señala Alchourrón que, en la concepción ideal que presenta, esto es, la del Sistema Maestro, la adecuación de la justificación depende del cumplimiento de dos condiciones: "(1) el contenido de una decisión debe ser una consecuencia lógica de las premisas que la fundamentan, y (2) las premisas normativas empleadas en la justificación deben ser generales".

Este concepto de justificación coincide con el expuesto en Alchourrón y Bulygin (1971), donde es presentado con mayor detalle.

Allí afirman los autores que la obligación del juez de fundar sus sentencias en derecho consiste en mostrar que la solución que da para el caso individual "deriva" de las normas generales del sistema, "de acuerdo con las reglas de inferencia del sistema". Explican que el juez tiene que dar una solución, i.e. formular un enunciado deóntico (Op, Pp, etc.), "[p]ero, como lo que tiene que solucionar es un caso individual, la solución que figura en la conclusión (parte dispositiva) de una sentencia normativa tiene que ser una solución individual (...) La justificación de una solución individual consiste en mostrar que ella deriva de una solución genérica. Por lo tanto, la fundamentación de una sentencia normativa es su derivación del sistema normativo (sistema que correlaciona casos genéricos con soluciones genéricas)" [p.212].

Según su análisis, la fundamentación de la sentencia comprende las siguientes operaciones: a) clasificación o subsunción del caso individual en algún caso genérico; b) determinación de la solución (genérica) que el sistema normativo correlaciona al caso genérico; c) derivación de la solución para el caso individual mediante las reglas de inferencia del sistema.

Dentro de este marco, que el contenido de una decisión resulte justificado o no parece depender de dos factores: a) cuáles sean las reglas de inferencia del sistema de que se trate, y b) cómo se analice la estructura lógica de los enunciados que figuran en las premisas y en la conclusión del razonamiento justificante del juez.

Con relación al segundo punto, en la obra a que me vengo refiriendo se presenta a las normas jurídicas generales —que constituirían las premisas normativas del razonamiento justificante— como enunciados que atribuyen determinadas consecuencias normativas a la presencia de ciertas circunstancias fácticas que se describen genéricamente mediante la mención de algunas propiedades. ¹ Las consecuencias normativas consisten en acciones descriptas también de modo genérico y caracterizadas deónticamente como obligatorias, prohibidas o permitidas. El razonamiento justificatorio consiste en una especie de silogismo donde una de las premisas es una norma general, la otra es un enunciado descriptivo que afirma la presencia de las circunstancias fácticas mencionadas en la norma, y la conclusión consiste en una norma categórica cuyo contenido es una particularización de la consecuencia normativa prevista en la norma general.

La relación entre las premisas y la conclusión es deductiva, de modo que la verificación de las circunstancias fácticas mencionadas en la norma general es condición suficiente para que se siga la conclusión.

Intuitivamente la idea parece bastante simple. Dada una norma general que establece, por ejemplo, que si alguien mata a otro debe sufrir una pena de veinte años de prisión, y dado un enunciado fáctico que afirma que Tulio mató a Sergio, aparentemente podríamos deducir que Tulio debe sufrir una pena de veinte años de prisión. una decisión judicial que tuviera este último contenido resultaría, entonces, justificada sobre la base de las premisas mencionadas.

En ese sentido, también MacCormick (1978), por ejemplo, considera indiscutible que, al menos en algunos casos —aunque no siempre—, se puede justificar una decisión judicial por medio de un argumento puramente deductivo: "dado que los tribunales hacen 'hallazgos fácticos' y que estos, sean realmente correctos o no, cuentan para los propósitos jurídicos como verdaderos; dado que las normas pueden (al menos a veces) ser expresadas en la forma 'si p entonces q' y dado que, al menos a veces, es el caso que los 'hechos' encontrados son inequívocamente instancias de 'p'; se sigue que a veces es el caso que una conclusión jurídica puede ser derivada válidamente por lógica deductiva de una formulación normativa y una proposición de hecho que sirven como premisas, y, consiguientemente, una decisión judicial que hace efectiva esa conclusión normativa está justificada por referencia a tal argumento" [p. 37].

Es importante advertir que la tesis de MacCormick parece obvia porque está presentada como un caso de aplicación de la regla del modus ponens. Sin embargo, para que esta regla pueda aplicarse es necesario que la premisa normativa tenga determinada forma lógica. Esto —la forma de la premisa normativa— constituye un aspecto esencial de la concepción deductivista, y es precisamente el punto en que centraré mi análisis crítico.

No obstante, antes de comenzar mi tarea crítica, en lo que resta de este apartado mencionaré, al solo efecto de descartarlas y prevenir confusiones con respecto al blanco de mi ataque, otras posibles objeciones que podrían eventualmente plantearse contra esa concepción.

Puede argüirse, sobre la base de precedentes judiciales y doctrinarios, que la concepción deductivista de la fundamentación de las sentencias no refleja adecuadamente los criterios que utilizan normalmente los jueces y juristas para evaluar los argumentos con que se pretende justificar una decisión judicial.

En ese sentido, si se analizan, por ejemplo, los precedentes de la Corte Suprema de Justicia de la Argentina, es fácil encontrar muchos casos en los que el defecto atribuido a una sentencia, en virtud del cual se la ha considerado arbitraria, es precisamente que ésta había incurrido en lo que el tribunal consideró un rigor excesivo en los razonamientos.

Así, ha dicho el alto tribunal que "el rigor de los razonamientos lógicos debe dejarse de lado ante la necesidad de no desvirtuar los fines que las leyes persiguen" (Fallos: 290:288; 292:357, entre otros); que "es contraria a derecho una interpretación de las normas realizada con rigor formal en los razonamientos, de tal modo que desvirtúa el espíritu de la ley" (Fallos: 304:134 y 1397), y que "no es siempre un método recomendable de interpretación de la ley el atenerse estrictamente a sus palabras, ya que el espíritu que informa la disposición es lo que debe determinarse en procura de su aplicación racional, que a la vez que elimine el riesgo de un formalismo paralizante, permita a los jueces superar las posibles imperfecciones técnicas de su instrumentación legal y dar pleno efecto a la intención del legislador" (Fallos: 306:940, 1059, 1462).

Sin embargo, los argumentos de ese tipo, aparentemente incompatibles con la concepción deductivista, pueden ser reconstruidos plausiblemente como una crítica al criterio de selección de las premisas normativas utilizadas por el juez. Podría sostenerse que en los precedentes transcriptos se confunden dos problemas diferentes: por un lado, el de identificar las normas en que se basará la decisión y, por otro, derivar la solución para el caso individual una vez identificadas las soluciones establecidas por las normas generales del sistema.

En efecto, la identificación de las premisas normativas no constituye, desde luego, una operación lógica, ni consiste exclusivamente, puede sostenerse, en identificar los textos sancionados por el legislador, sino en interpretar su sentido, para lo cual el juez puede ser guiado por consideraciones de variada índole. En ese orden de ideas, cabe señalar que Alchourrón y Bulygin han afirmado en diversos trabajos que no conciben a las normas como entidades lingüísticas —oraciones de cierto tipo— sino como el significado de ciertas expresiones lingüísticas, y han distinguido claramente las normas de las formulaciones normativas. Mientras estas últimas son oraciones susceptibles de diversas interpretaciones, habida cuenta de la vaguedad y ambigüedad características del lenguaje ordinario, las normas son el resultado de determinada interpretación de las formulaciones normativas, que resulta no sólo del significado que se atribuya a los términos de cada formulación en particular, por ejemplo cada artículo de un código, sino también del alcance que se les acuerde teniendo en cuenta lo dispuesto en otras formulaciones normativas.

Por ejemplo, si se han sancionado las siguientes formulaciones normativas:

a) Si alguien mata a otro debe ser castigado con prisión perpetua;

b) Los menores de edad no deben ser castigados; el resultado de la interpretación puede ser una única norma que establezca:

Si alguien mata a otro y no es menor de edad debe ser castigado con prisión perpetua; o bien dos normas que dispongan:

a') Si alguien mata a otro debe ser castigado con prisión perpetua;

b') Los menores de edad no deben ser castigados, a menos que maten a otro. ²

Con tal marco de referencia, es fácil advertir que las críticas contenidas en los extractos de fallos de la Corte Suprema transcriptos pueden entenderse como dirigidas contra un criterio de interpretación de las formulaciones normativas que reflejaría un apego excesivo del juez —en opinión del alto tribunal— al sentido literal de las palabras empleadas por el legislador. Ahora bien, cualesquiera sean las razones por las que pueda considerarse desacertada la interpretación de un texto legal, parece claro que se trata de un problema relativo a la selección de las premisas, y no a la estructura formal del razonamiento justificatorio. Es que, como destaca Rodríguez (2002), "aunque sea correcto que para establecer las premisas de un argumento se debe recurrir muchas veces a interpretaciones, decisiones y valoraciones, ello no comporta obstáculo alguno a la idea de que el paso de las premisas a la conclusión puede ser siempre reconstruido como una inferencia deductiva" [p.254].

En efecto, parecería hasta trivial que, dada una decisión judicial, siempre es posible construir un silogismo en el que el contenido de la decisión resulte implicado por ciertas premisas normativas y fácticas, a menos que existan restricciones claras respecto de los métodos admisibles para la obtención de las premisas.

Sin embargo, planteada la cuestión de esa manera, puede también apreciarse que la defensa de la concepción deductivista tiene autonomía con respecto a los ideales en que se enmarca la llamada 'concepción del Sistema Maestro' a los que me referí al comienzo de este apartado. Ello es así porque las reglas son accesibles a los ciudadanos a través de los textos legislados, esto es, de las formulaciones normativas emitidas por el legislador. Sin embargo, el legislador no controla la interpretación que de tales textos hagan los jueces, ni el conocimiento de ellos por los ciudadanos garantiza que estos puedan conocer el alcance de sus derechos y obligaciones antes de que los textos sean interpretados por los jueces. Por último, nada garantiza que los jueces coincidan en la interpretación —ni que identifiquen los mismos textos como relevantes— o aun que cada juez los interprete siempre de la misma manera. Es claro, por consiguiente, que la concepción deductivista de las sentencias es compatible con la frustración de los ideales de democracia, igualdad y certeza que dan apoyo a la doctrina de la separación de poderes.

Con todo, debe remarcarse que lo expresado en el párrafo anterior no pretende ser una crítica a la concepción deductivista. En ese sentido, es del caso destacar que los autores que he identificado como sus defensores paradigmáticos nunca sostuvieron que de hecho los ideales del Sistema Maestro se cumplieran, ni mucho menos, que la concepción deductivista garantizara su cumplimiento. Sin embargo, conviene tenerlo presente para prevenir posibles confusiones con respecto al alcance práctico de tal concepción.

En otro orden de ideas, debe también descartarse una posible objeción a la concepción deductivista que se funde en el hecho de que a veces los jueces, una vez identificadas las normas jurídicas aplicables al caso, deciden, por alguna razón —incluso por buenas razones—, prescindir de ellas. En efecto, que en alguna ocasión puedan invocarse razones atendibles para no fallar de acuerdo con las normas del sistema jurídico no evidencia un defecto de dicha concepción. La situación se puede describir simplemente como un caso en el que la decisión no ha sido fundada en derecho y, en ese sentido, es arbitraria. ³

III. La forma lógica de las normas generales.

Como ya anticipé, mi crítica a la concepción deductivista se centra en la forma lógica que esa concepción necesita atribuir a las normas generales. Para enmarcar adecuadamente la cuestión, comenzaré por recordar algunos aspectos básicos del llamado 'sistema standard de lógica deóntica' y presentaré una semántica para ese sistema. Luego utilizaré esos elementos para hacer algunas distinciones relevantes.

A) El sistema standard de lógica deóntica:

Como es sabido, existen diversos sistemas de lógica deóntica. Entre ellos, el denominado 'sistema standard' o 'sistema D' es el más cercano a la lógica modal, pues puede ser obtenido a partir del más débil de los sistemas modales, que es el llamado 'sistema K, mediante la introducción de muy pocas modificaciones, como mostraré a continuación.

El sistema K de lógica modal se obtiene agregando a la lógica proposicional clásica el axioma esquema:

AK: N(A→B) → (NA→NB) —donde 'N' es el operador de necesidad—, la definición del operador de posibilidad (M) a partir del de necesidad:

Def.M: MA =_Df ¬N¬A

y la regla de inferencia llamada 'regla de necesitación', de acuerdo con la cual, si A es un teorema, NA también lo es:

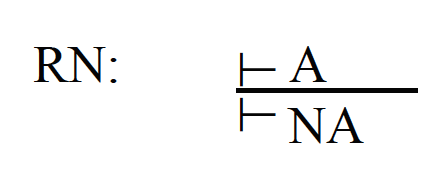
Todos los sistemas que son extensiones de K —como los sistemas T, S4, S5, entre muchos otros—, así como K mismo, se conocen como 'sistemas modales normales'.

Se puede obtener una versión deóntica del sistema K mediante la sustitución de N por el operador de obligación (O) y de M por el de permisión (P), con lo cual el axioma, la definición y la regla de inferencia antes presentadas quedan formulados de la siguiente manera:

AKO: O(A→B) → (OA→OB)

Def. P: PA =_Df ¬O¬A

y la regla de inferencia llamada 'de necesitación deóntica':

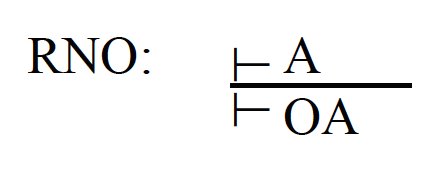
El sistema así obtenido constituye lo que Åqvist (1984, p. 615) llama 'lógica deóntica proposicional monádica normal de tipo von Wright'. Para obtener el sistema standard es suficiente con agregar el siguiente axioma esquema:

ADO: OA→PA ⁴

B) Una semántica para el sistema standard de lógica deóntica:

En lógica modal, es usual recurrir a la teoría de modelos, tal como ha sido desarrollada a partir de los trabajos de Kripke (1963), para construir semánticas adecuadas para la interpretación de los diversos sistemas modales.

Un modelo de Kripke para la lógica proposicional modal consiste en una terna ordenada <M, R, V>, donde M es un conjunto no vacío de mundos posibles {m₁ m₂, ..., m_n}, R es una relación entre los elementos de M, llamada 'relación de accesibilidad', que puede describirse como una relación de posibilidad relativa, y V es una función de valuación que determina el valor de verdad de cada enunciado en cada mundo del conjunto M. La función de valuación hace corresponder un valor de verdad a cada par {A, m_i} formado por un enunciado y un mundo del conjunto M.

A continuación indico las condiciones que debe cumplir toda función de valuación. A tal efecto, utilizo expresiones de tipo 'V(A, m_i)' para referirme al valor de verdad que la función de valuación V hace corresponder al enunciado A en el mundo mi Las expresiones de tipo 'm_iRm ' significan que el mundo m_j es accesible al mundo mi por la relación de accesibilidad R.

1. Para todo enunciado atómico A y mundo m_i ∈ M, V(A, m_i) = 1 (verdad) o V(A, m_i) = 0 (falsedad).

2. Para todo enunciado A y mundo m_i ∈ M, V(¬A, m_i) = 1 si y sólo si V(A, mi) = 0

3. Para todo par de enunciados A, B, y mundo m_i ∈ M, V(A^B, m_i) = 1 si y sólo si V(A, m_i) = 1 y V(B, m_i) = 1

4. Para todo par de enunciados A, B, y mundo m_i ∈ M, V(AvB, m_i) = 1 si y sólo si V(A, m_i) = 1 o V(B, m_i) = 1

5. Para todo par de enunciados A, B, y mundo m_i ∈ M, V(A→B, m_i) = 1 si y sólo si V(A, m_i) = 0 o V(B, m_i) = 1

6. Para todo enunciado A y mundo m_i ∈ M, V(NA, m _i) = 1 si y sólo si para todo mundo m_j tal que m_iRm_j, V(A, m_j) = 1

7. Para todo enunciado A y mundo m_i ∈ M, V(MA, m_i) = 1 si y sólo si hay al menos un mundo m_j tal que m_iRm_j y V(A, m_j) = 1

Que un enunciado A es satisfacible en un modelo <M, R, V> significa que A es verdadero en algún mundo m_i∈M. Que un conjunto de enunciados es satisfacible en un modelo <M, R, V> significa que hay un mundo m_i∈M en el cual son verdaderos todos los enunciados de ese conjunto.

Que un enunciado A es válido en un modelo <M, R, V> significa que A es verdadero en todo mundo m_i∈M.

La anterior definición de validez está ligada a una función de valuación determinada. Para dar una noción de validez más general es necesario introducir la noción de marco.

Un marco es un par ordenado <M,R,>, donde M es un conjunto no vacío de mundos y R es una relación de accesibilidad entre mundos. Si V es una función de valuación definida en el marco <M, R>, es decir, que asigna valores de verdad a cada enunciado del lenguaje de que se trate en cada mundo perteneciente a M y en conformidad con las relaciones de accesibilidad determinadas por R, se dice que <M, R, V> es un modelo basado en el marco <M, R>.

Se dice que un enunciado A es válido en un marco <M, R> si y sólo si A es válido en todo modelo basado en el marco <M, R>. Asimismo, A es válido en una clase de marcos si y sólo si A es válido en todos los marcos de esa clase.

Por último, se dice que un enunciado A es K-válido si y sólo si A es válido en todo marco.

De las definiciones precedentes se desprende que si un enunciado es válido en una clase de marcos, su negación no es satisfacible en ningún modelo de la clase de marcos de que se trate, y conversamente, si un enunciado no es válido, su negación es satisfacible.

Un enunciado A es consecuencia semántica de un conjunto de enunciados Γ en una clase de marcos si y sólo si Γ∪{¬A} no es satisfacible en ningún modelo de esa clase de marcos.

Se puede probar, aunque no es necesario hacerlo aquí, que la clase de los enunciados K-válidos coincide con la clase de los teoremas del sistema K. ⁵ En otras palabra, el sistema K es adecuado con relación a la noción de K-validez porque todo teorema del sistema K es K-válido, y el sistema es completo con relación a esa noción de K-validez porque todo enunciado K-válido es demostrable como teorema en K.

Mediante la introducción de diversas condiciones a la relación R, tales como reflexividad, simetría, transitividad, etc., se puede restringir la clase de marcos con relación a los cuales se define la validez. Con ese procedimiento es posible dar definiciones de validez adecuadas para cada sistema modal normal.

De manera similar, es posible establecer las condiciones de satisfacibilidad de un conjunto de enunciados normativos sobre la base de modelos semánticos, los que pueden ser concebidos, al igual que en lógica modal, como ternas ordenadas <M, R, V> que representan un conjunto de mundos, una relación de accesibilidad y una función de valuación.

Las intuiciones orientadoras para establecer en qué condiciones un conjunto de enunciados normativos es satisfacible son las siguientes: (i) cuando decimos que una acción o estado de cosas p está permitido, no estamos afirmando que de hecho se da ese estado de cosas o se realiza esa acción en el mundo real, sino que estamos, más bien, admitiendo la posibilidad de que se transforme el mundo real en otro en que p sea el caso sin que ello determine el incumplimiento de ninguna obligación. (ii) Similarmente, cuando afirmamos que una acción o estado de cosas p es obligatorio, no decimos que se da en el mundo real, sino que estamos poniendo el mundo real en relación con otro mundo ideal en que p es el caso. Entonces, podemos pensar que un conjunto de enunciados deónticos — es satisfacible en un modelo determinado si es posible poner algún mundo de ese modelo, digamos m_i, en relación con otros mundos tales que en ellos se cumplen todas las obligaciones y, a la vez, para cada permisión hay al menos uno en que se hace uso de ella. Los mundos accesibles a un mundo dado se denominan 'alternativas deónticas', y son concebidos como mundos ideales o deónticamente perfectos con relación a dicho mundo. La relación R es una relación de alternatividad deóntica y la fórmula 'm_iRm_j' expresa que mj es una alternativa deóntica de m_i.

Sobre la base de esas ideas, la definición de las condiciones de verdad de los enunciados de obligación resulta similar a la de los enunciados de necesidad, y la definición de las condiciones de verdad de los enunciados de permisión resulta similar a la de los de posibilidad. ⁶ Esto significa que las únicas modificaciones que es necesario hacer a las reglas dadas anteriormente para las funciones de valuación de un modelo de Kripke consisten en sustituir 'NA' por 'OA' en la regla 6 y 'MA' por 'PA' en la regla 7, con lo que quedan formuladas de la siguiente manera:

6'. Para todo enunciado A y mundo m_i ∈ M, V(OA, m_i) = 1 si y sólo si para todo mundo mj tal que m_iRm_j, V(A, m_j) = 1

7'. Para todo enunciado A y mundo m_i ∈ M, V(PA, m_i) = 1 si y sólo si hay al menos un mundo m_j tal que m_iRm_j y V(A, m_j) = 1

Como ya señalé, el sistema standard se obtiene mediante el agregado del axioma esquema ADO (OA→PA). Para que los enunciados de esa forma resulten válidos, basta con introducir como restricción a la relación de accesibilidad R la exigencia de que R sea serial. Ese requisito consiste en que para todo mundo hay una alternativa deóntica: Para todo m_i∈M existe un m_j∈M —no necesariamente distinto de mi— tal que m_iRm_j. Con esa restricción, resultan válidas —en la clase de marcos que ella define— todas y sólo las fórmulas del sistema standard. ⁷

El agregado o modificación de las restricciones que se imponen a R permite obtener distintos sistemas de lógica deóntica. Por ello, la elaboración de un sistema de lógica deóntica puede comenzar por la reflexión sobre nuestras intuiciones acerca de cómo deberían construirse las alternativas deónticas. Éste ha probado ser un método muy fructífero, que permite advertir ambigüedades e imprecisiones en el uso de los conceptos deónticos y resulta de utilidad para analizar la forma lógica de los enunciados normativos del lenguaje natural. ⁸

C) Consistencia e inconsistencia normativa:

La semántica presentada, aunque muy simple, es suficiente para descubrir algunas falacias en que se incurre frecuentemente en el razonamiento normativo. En este apartado presentaré distinciones vinculadas al concepto de contradicción normativa y mostraré errores relativos al alcance de ese concepto, que se producen al extraer conclusiones normativas a partir de la combinación de enunciados normativos con enunciados fácticos.

En primer lugar, sobre la base de las nociones expuestas, precisaré el sentido de algunas expresiones:

Se dirá que un conjunto de enunciados deónticos no es satisfacible en una clase de marcos si no hay ningún modelo de esa clase en el cual ese conjunto sea satisfacible, es decir, en ningún modelo hay un mundo posible m_i tal que todos los enunciados del conjunto son verdaderos en ese mundo. como vimos también, la verdad de los enunciados deónticos depende de su relación con otros mundos posibles que cumplan con las condiciones de alternatividad deóntica.

Por otro lado, un conjunto de enunciados Γ es inconsistente en un sistema S si hay un subconjunto {p₁, ..., p_n} de Γ tal que ¬(p₁∧ ... ∧p_n) es un teorema de S. Si S es adecuado y completo con relación a una clase de marcos, todo conjunto de enunciados inconsistente es insatisfacible en esa clase de marcos y todo conjunto insatisfacible es inconsistente.

Es importante poner de relieve que todo mundo lógicamente posible puede formar parte de un modelo. Por tanto, cuando nos preguntamos si un conjunto de normas es satisfacible, no debemos restringir la consideración a los mundos empíricamente posibles o a aquéllos que tengan en común con el mundo real ciertas circunstancias fácticas o relaciones causales.

Por ejemplo, ¿forman un conjunto insatisfacible la norma que permite a Shylock cortar una libra de carne del cuerpo de Antonio y la que le prohíbe derramar la sangre de Antonio?

Sin duda hay un mundo lógicamente posible en el que Shylock corta la carne de Antonio y no derrama su sangre. Por tanto, puesto que no hay inconvenientes en que un modelo admita ese mundo, el par de normas es satisfacible —no hay inconveniente en que en todos los mundos accesibles a un mundo determinado Shylock observe la prohibición de derramar sangre y, al mismo tiempo, en uno de ellos haga uso de la permisión de cortar la libra de carne—.

Es verdad que Shylock no puede, de hecho, cortar la carne sin derramar sangre. Sin embargo, parece claro que debe hacerse una distinción entre la imposibilidad fáctica y la lógica, porque la consistencia y la inconsistencia son temas de la lógica, que es una disciplina apriorística.

En respaldo de la necesidad de hacer esa distinción debe observarse que no es indispensable que haya más de una norma para que se produzca el tipo de imposibilidad fáctica en consideración. Bastaría con que una norma general estableciera la obligatoriedad de un tipo determinado de acción, como muestra el siguiente ejemplo: ⁹

Un médico que presta servicios en un distrito rural se encuentra regido por un código que contiene la siguiente norma, que llamaré n₁: Si algún habitante del distrito informa que ha sufrido un ataque cardíaco, el médico debe visitarlo en el plazo de una hora.

En una ocasión, los habitantes del distrito que llamaremos 1, 2 y 3 solicitan la atención del médico por haber sufrido sendos ataques cardíacos. Dada la distancia a que vive uno de otro, el médico está en condiciones de atender, dentro del plazo de una hora, o bien a los habitantes 1 y 2 o bien al habitante 3. Si atiende a 3, no puede atender en término a 1 ni a 2.

Podría pensarse que la exigencia contenida en la norma impone al médico deberes incompatibles, puesto que de ella parece desprenderse que tiene el deber de atender a 1 y 2, para lo cual tiene que dejar de atender a 3, y que tiene el deber de atender a 3, para lo cual tiene que dejar de atender a 1 y 2. Sin embargo, por otro lado, la norma no parece contener ninguna contradicción en sus términos, por lo cual parecería extraño que resultara insatisfacible. A mi modo de ver, la cuestión debe analizarse como sigue:

Asumiré —sin discusión por el momento— que la forma lógica de la norma es 'OA', y que la forma lógica del enunciado que ocupa en el ejemplo el lugar de 'A' es '∀x(Fx→Gmx)', donde 'Fx' está por: 'x informa haber sufrido un ataque cardíaco' y 'Gmx' está por 'el médico atiende a x'. Por tanto, la norma puede representarse de la siguiente manera:

n₁:O∀x(Fx→Gmx) ¹⁰

Es claro que el enunciado universal '∀x(Fx→Gmx)' implica 'F1→Gm1', 'F2→Gm2' y 'F3→Gm3', por lo que pueden inferirse las siguientes normas derivadas: ¹¹

n₂: O(F1→Gm1)

n_3: O(F2→Gm2)

n₄: O(F3→Gm3)

Para que esas tres normas sean verdaderas en un mundo determinado, lo único necesario es que en todos los mundos accesibles a aquél sean verdaderos los condicionales: 'F1→Gm1', 'F2→Gm2' y 'F3→Gm3'. En consecuencia, los mundos accesibles serán aquéllos en que es verdad una de las siguientes conjunciones:

m₁: F1∧F2∧F3∧Gm1∧Gm2∧Gm3;

m₂: F1∧F2∧¬F3∧Gm1∧Gm2∧¬Gm3;

m₃: F1∧¬F2∧F3∧Gm1∧¬Gm2∧Gm3;

m₄: ¬F1∧F2∧F3∧¬Gm1∧Gm2∧Gm3;

m₅: F1∧¬F2∧¬F3∧Gm1∧¬Gm2∧¬Gm3;

m₆: ¬F1∧F2∧¬F3∧¬Gm1∧Gm2∧¬Gm3;

m₇: ¬F1∧¬F2∧F3∧¬Gm1∧¬Gm2∧Gm3

m₈: ¬F1∧¬F2∧¬F3∧¬Gm1∧¬Gm2∧¬Gm3

y algunas otras variaciones triviales que omitiré, en las que el médico atiende también a pacientes que no lo han llamado, además de atender a los que lo llamaron, como en m₉:

m₉: F1∧F2∧¬F3∧Gm1∧Gm2∧Gm3; (...)

Por otro lado, los mundos que no son accesibles son aquéllos en que es verdadera al menos una de las siguientes conjunciones:

m': F1∧¬Gm1;

m": F2∧¬Gm2;

m'": F3∧¬Gm3

Como se ve, las normas son satisfacibles, ya que no hay inconvenientes en construir un modelo en el que los únicos mundos accesibles a un mundo determinado sean m₁-m₉ o algún subconjunto no vacío de ellos. Lo que ocurre es que, dado que en el mundo del ejemplo, donde rigen las normas n₁-n₄, es de hecho verdadera la conjunción F1∧F2∧F3, tal vez no exista manera de transformar ese mundo en uno de los accesibles, porque no sea posible pasar a un mundo donde no sea verdad F1 o F2 o F3 ni tampoco sea técnicamente alcanzable el mundo m₁, que es el único de los accesibles compatible con esa conjunción. Sin embargo, es claramente distinguible la cuestión de si las normas son satisfacibles –y, por ende, consistentes– del problema de alcanzar de hecho algún mundo deónticamente perfecto, es decir, de hacer realidad el ideal deóntico que plantean las normas.

Adviértase que, si se considerara que el conjunto {n₂, n₃, n₄}es insatisfacible, y por tanto, inconsistente, y que, por ende, también lo es la norma n₁, que lo implica, debería concluirse que el médico no tiene ninguna obligación. Sin embargo, esto resultaría algo extraño. Es posible que en el caso presente el médico decida atender a 1 y 2, o que decida atender solamente a 3, o incluso, que se quede cruzado de brazos, ante la imposiblidad de cumplir, haga lo que haga, con la norma n₁. Pero, cualquiera sea la decisión que adopte, lo cierto es que no esperaríamos que en otros supuestos, por ejemplo cuando sólo sufre un ataque cardíaco el habitante 5, el médico no lo atienda alegando que la norma n₁ es inconsistente.

En suma, es verdad que de hecho el médico no puede atender a los tres, pero esto sólo significa que el mundo real es tal que no es de hecho posible transformarlo en ninguno de los mundos ideales. sin embargo, la pregunta sobre qué ha de hacer el médico cuando no es posible de hecho cumplir con sus obligaciones parece diferente de la pregunta sobre qué debe hacer cuando las normas que lo rigen son inconsistentes. Para advertirlo basta con considerar que si la norma fuera inconsistente podría simplemente descartarla —en forma definitiva—, mientras que ese no parece ser el caso cuando establece obligaciones que de hecho no pueden ser totalmente satisfechas en alguna oportunidad. Las normas inconsistentes no son inteligibles, ya que no postulan ningún ideal, es decir, no hay ningún mundo deónticamente perfecto asociado a ellas. Por tanto, tampoco es posible tratar de hacer real un mundo que se parezca lo más posible al ideal deóntico, puesto que no hay tal ideal.

Veamos ahora los aspectos formales de las cuestiones planteadas.

La derivación de una contradicción normativa, en el caso de Shylock, entre la norma que lo autoriza a cortar la carne de Antonio y la que le prohíbe derramar sangre, supone que la prohibición de derramar sangre implica –en las circunstancias– la prohibición de cortar carne, don-de por 'en las circunstancias' se entiende el hecho de que sea verdadero el condicional material: 'si Shylock corta la carne de Antonio entonces Shylock derrama la sangre de Antonio'. En términos generales, la estructura del razonamiento consiste en derivar, a partir de la premisa normativa 'O¬q' y la premisa fáctica 'p→q', la conclusión 'O¬p'. Para mostrar que se trata de un razonamiento falaz, conviene comenzar por señalar que el condicional 'p→q' es lógicamente equivalente a '¬q→¬p', de modo que la aceptación del razonamiento en cuestión importa aceptar como verdad lógica '(O¬q∧(¬q→¬p))→O¬p'. Esto, a su vez, tiene la forma general '(OA∧(A→B))→OB'.

Mostraré que la aceptación de la validez de ese esquema tiene consecuencias absurdas:

Lo que afirma 16 es que si algo es obligatorio, entonces todo lo que de hecho ocurre es obligatorio. Esta consecuencia es manifiestamente inadmisible, por lo que debe rechazarse la validez del esquema del que deriva.

D) Dos concepciones de las normas condicionales:

En el apartado anterior asumí sin discusión que las condiciones de verdad de las normas en juego eran las correspondientes a las de forma 'OA', con total independencia de cuál fuera la estructura de la fórmula que ocupara el lugar de 'A'. como, en el caso de las normas derivadas n₂, n₃ y n₄, la forma lógica de la proposición que ocupa el lugar de 'A' es la condicional, la forma expandida de las normas es 'O(B→C)'. Sin embargo, el hecho de que el contenido normativo tenga estructura condicional no produce modificación en cuanto a la caracterización semántica de las condiciones de verdad de la norma: para que la norma sea verdadera, la proposición que está caracterizada como obligatoria debe ser verdadera en todos los mundos accesibles. si la proposición en cuestión es un condicional, sus condiciones de verdad son, obviamente, las que corresponden a una proposición de esa forma, pero eso no importa dar un tratamiento diferenciado a las normas cuyo contenido es condicional.

Sin embargo, algunos autores considerarían más adecuado representar la forma lógica de las normas condicionales, como, por ejemplo, la que establece 'si el habitante 1 se enferma, el médico debe atenderlo', mediante fórmulas mixtas de tipo 'A→OB', donde el operador deóntico afecta sólo al consecuente. Alchourrón (1996 b), es un firme defensor de esta última concepción, a la que ha denominado 'concepción puente" porque en ella las normas condicionales son "como puentes que conectan lo que es (o podría ser) el caso y lo que debe ser (hecho)".

La defensa de la concepción puente se encuentra esencialmente vinculada a la concepción deductivista de las sentencias judiciales. En efecto, resulta indispensable analizar la forma lógica de las normas generales de acuerdo con los lineamientos de la concepción puente para poder justificar el tipo de relación deductiva requerido por ese concepto de fundamentación.

Ello es así porque la regla de inferencia que permite derivar la conclusión no es otra que la de separación o modus ponens, la cual, cuando opera en contextos normativos, ha sido denominada por Alchourrón (1993) 'modus ponens deóntico'. Esta regla permite derivar el consecuente de un condicional cuando entre las premisas figura, además del condicional, su antecedente. De ese modo, puede deducirse una norma categórica —digamos 'OA'— a partir de una premisa normativa de la forma 'A→OB' y la premisa fáctica 'A'.

Por oposición, los diversos análisis de las normas condicionales que no admiten ese tipo de derivación —entre los que está el de la lógica standard—han sido englobados por Alchourrón bajo la denominación: 'concepción insular', porque en ella todos los elementos de las normas "están referidos al reino del deber".

IV. Críticas a la concepción puente.

Expondré aquí algunos argumentos en contra de la concepción puente de las normas condicionales.

Primera observación:

En primer lugar debe señalarse que las fórmulas mixtas, del tipo 'A→OB', que son una composición veritativo funcional de un enunciado descriptivo y uno normativo, no pueden ser consideradas fórmulas bien formadas en el sistema clásico de von Wright (1951), porque allí los términos descriptivos no deónticos no son oraciones sino nombres de acciones genéricas. ¹² Por tanto, como 'A' no representa una proposición sino un nombre, al ligarla con una proposición por medio de una conectiva no obtenemos otra proposición sino una expresión sin sentido. En ese enfoque, los términos deónticos se comportan como predicados, que, unidos al nombre de una acción genérica, forman una oración.

En el sistema standard, en cambio, las fórmulas a las que se aplican los términos deónticos son oraciones, es decir que expresan proposiciones. Por tanto, los términos deónticos se entienden como operadores: operan en proposiciones y resultan en proposiciones.

Si bien en el sistema standard tampoco aparecen fórmulas mixtas, no existe el mismo tipo de inconveniente que en el sistema clásico. No obstante, la admisión de fórmulas de ese tipo es pasible de la siguiente objeción:

El análisis de la forma lógica de un enunciado exige diferenciar diversas categorías sintácticas de expresiones: por un lado, las constantes lógicas; por otro, el resto de las expresiones. Dentro de este último grupo se puede distinguir distintas subcategorías: oraciones, expresiones predicativas y términos individuales, además de las expresiones auxiliares. La distinción de categorías sintácticas es relevante para determinar las formas de combinación de todas esas expresiones que dan lugar a fórmulas bien formadas y oraciones, ya que, si dos expresiones pertenecen a la misma categoría sintáctica, el resultado de reemplazar una de ellas por la otra en una fórmula bien formada es también una fórmula bien formada.

Paralelamente a la clasificación en categorías sintácticas, las expresiones de un lenguaje pueden también agruparse en distintas categorías semánticas. En ese sentido, se dice que dos expresiones pertenecen a la misma categoría semántica si, y sólo si, las reglas de interpretación les asignan el mismo tipo de entidad (individuos, extensiones, valores de verdad) o bien se encuentran regidas por el mismo tipo de reglas de interpretación (por ejemplo, a las conectivas de la lógica proposicional se aplican reglas que fijan el valor de verdad de las oraciones compuestas mediante su empleo sobre la base de los valores de verdad de las componentes).

Se dice que un lenguaje es transparente cuando sus categorías sintácticas y semánticas coinciden, es decir, cuando todas las expresiones de la misma categoría sintáctica pertenecen a la misma categoría semántica y viceversa.

Precisamente, la diferencia principal entre los lenguajes naturales y los artificiales que utiliza la lógica es que estos últimos son transparentes. como consecuencia, en ellos se exhibe claramente la forma lógica, ya que se encuentran fijadas todas las distinciones necesarias y las combinaciones admisibles, mientras que en los primeros eso no ocurre. Por eso, en un lenguaje artificial es posible establecer relaciones de deducción y formular reglas de derivación tomando en cuenta sólo el aspecto físico de las fórmulas.

Desde esta perspectiva, el análisis de las normas condicionales que ofrece la concepción puente parece difícil de aceptar para quienes, como Alchourrón, no admiten que tenga sentido atribuir valores de verdad a las normas. En efecto, de ser ello así, resultaría que el lenguaje resultante permite que el condicional ligue entidades que pertenecen a distintas categorías semánticas, ya que a la izquierda aparece una oración descriptiva, a la que se puede asignar valores de verdad, y a la derecha, una expresión a la que no tiene sentido asignar tales valores. Por otro lado, debe admitirse que tanto las oraciones deónticas como las descriptivas pertenecen a la misma categoría sintáctica (oraciones), pues de lo contrario no se obtendría una fórmula bien formada al ligarlas mediante una conectiva. sin embargo, al sustituir en el lado derecho del signo condicional una oración deóntica por una descriptiva, el resultado que se obtiene pertenece a una categoría semántica diferente: ahora ya no expresa una norma sino una descripción y, por ende, tiene valor de verdad. En consecuencia, el lenguaje no es transparente, ya que al sustituir unos elementos por otros de la misma categoría sintáctica se obtienen resultados de distinta categoría semántica. ¹³

Segunda observación:

La concepción puente y la insular son incompatibles. Si se las combina se obtienen consecuencias paradójicas.

Por ejemplo, considérese el siguiente conjunto de fórmulas aparentemente consistente:

1) ¬p

2) ¬p→O¬q

3) Op

4) O(p→q)

De 1) y 2) se sigue, por modus ponens,

5) O¬q

A la vez, en todo sistema de lógica deóntica normal, es decir, que cumple con AKO, es válido:

6) (O(p→q)∧Op)→Oq

Por tanto, de 3) y 4) se sigue:

7) Oq

Finalmente, de 5) y 7) se sigue la contradicción deóntica:

8) Oq∧O¬q

lo que implica que el conjunto de las premisas 1), 2) 3) y 4) no es consistente. Esto significa que, en un mundo donde sean verdaderas las normas 2), 3) y 4), ¬p es un hecho imposible, lo que es absurdo [conf. Åqvist, 1984].

Parecería, entonces, que si se desea defender la concepción puente, las reglas de formación deberían excluir las fórmulas de la forma O(A→B). Sin embargo, éstas son fórmulas bien formadas en la lógica deóntica standard. Por ende, la defensa de la concepción puente parece requerir el rechazo de aquélla. sin embargo, Alchourrón no da ese paso sino que, por el contrario, inserta la concepción puente dentro de la lógica deóntica standard (sistema D). ¹⁴

Por otro lado, la admisión de las fórmulas del tipo 'O(A→B)' resulta útil para analizar diversas cuestiones. Así, por ejemplo, se vio en el apartado III-C su empleo en el ejemplo del médico rural. Veremos ahora un conocido problema de la lógica deóntica:

El dilema de Jefté:

Considérese el siguiente argumento:

(1) Miriam (la hija de Jefté) = el primer ser que saldrá al encuentro de Jefté cuando él regrese a casa.

(2) Es obligatorio que Jefté inmole al primer ser que salga a su encuentro cuando él regrese a casa (porque lo prometió a Jehová).

Por tanto: Es obligatorio que Jefté inmole a Miriam.

Por otra parte, la ley divina le prohíbe a Jefté matar a sus hijos, de modo que parece que Jehová le impone deberes contradictorios. sin embargo, parece extraño que se deba concebir a Jehová como un legislador irracional.

De acuerdo con el análisis que propondré, las premisas son verdaderas, pero la conclusión es falsa, de modo que se trata de un argumento inválido.

Ante todo cuadra advertir que en las premisas aparece una descripción definida: 'el primer ser que salga a su encuentro cuando Jefté regrese a casa'. Ahora bien, en el lenguaje ordinario el uso de las descripciones definidas presenta una ambigüedad característica, que se suele identificar como 'uso referencial' y 'uso atributivo'. Ilustraré la distinción con el siguiente ejemplo:

i) Juan desea casarse con la mujer más hermosa del pueblo.

ii) Marta = la mujer más hermosa del pueblo.

Por lo tanto:

iii) Juan desea casarse con Marta.

¿Es correcto el razonamiento anterior?

La respuesta depende del sentido de la oración 'i)', ya que puede querer decir dos cosas muy distintas:

i') Juan tiene en mente a una mujer en particular —Marta—, a la cual el emisor de la oración se refiere como 'la mujer más hermosa del pueblo'.

i") Juan no tiene en mente a nadie en particular, pero desea casarse con quien resulte ser la más hermosa del pueblo, sea quien sea.

En el primer caso, el uso de la descripción definida es referencial, en el segundo caso, es atributivo. Cuando la descripción tiene uso referencial, se comporta como un nombre propio y puede ser sustituida por otro nombre o descripción sin que se altere el valor de verdad de la oración. En consecuencia, si el sentido de i) es el que se indica en i'), el razonamiento es correcto. En cambio, cuando el uso de la descripción definida es atributivo, el valor de verdad de la oración puede cambiar cuando se sustituye la descripción definida por el nombre del individuo que de hecho satisface la descripción o por otra descripción que es satisfecha por el mismo individuo. En este caso el razonamiento es incorrecto, porque el enunciado 'i)' no se refiere a Marta ni a nadie en particular, aunque de hecho haya una persona que satisfaga la descripción, y que esa persona sea precisamente Marta.

En el caso de Jefté, la descripción es atributiva: lo que Jefté prometió es inmolar a cualquiera que satisficiera esa descripción. En consecuencia, la premisa (2) no afirma que hay un individuo que satisface la descripción y que Jefté debe inmolar precisamente a ese individuo —por los motivos que fuere— sino que la obligación consiste en que inmole a quien eventualmente satisfaga la descripción.

En el análisis semántico parece claro que, si la premisa (2) es verdadera, en todos los mundos accesibles Jefté inmola a la persona que satisface la descripción, pues eso es lo que ha prometido. Sin embargo, quien satisface la descripción no tiene por qué ser el mismo individuo en todos los mundos accesibles, ya que es lógicamente posible que el primer ser que salga a su encuentro no sea Miriam sino cualquier otro. Por otro lado, si la conclusión es verdadera, Jefté mata a Miriam en todos los mundos accesibles. ¿se desprende esto de las premisas? Veamos:

Existen dos posibilidades obvias de formalización de la premisa (2), a saber:

(2') ∀x(∀y(Sy↔y=x)→OMax)

(2") O∀x(∀y(Sy↔y=x)→Max)

donde 'S' está por '— sale al encuentro de Jefté en primer lugar', 'M' está por '— inmola a —' y 'a' está por 'Jefté'.

De (2') se puede inferir ¹⁵

(3') ∀y(Sy↔y=b)→OMab

donde 'b' está por Miriam. Y como parece claro que la forma de (1) es:

(1') ∀y(Sy↔y=b)

la conclusión OMab (es obligatorio que Jefté inmole a Miriam) se deduce en virtud del modus ponens deóntico.

En cambio, de (2") se deduce:

(3") O(∀y(Sy↔y=b)→Mab)

pero de ésta y (1') no se puede deducir la conclusión OMab.

La diferencia, como es fácil advertir, es que la forma general de (3') es 'A→OB', mientras que la de (3") O(A→B). La primera corresponde a la concepción puente, mientras que la segunda, a la insular.

De la primera, junto con la premisa fáctica (1'), se puede inferir la norma categórica que expresa la conclusión.

La concepción insular, en cambio, no permite ese tipo de inferencias. De la conjunción de normas condicionales con enunciados fácticos no derivan normas categóricas. No obstante, en todos los mundos accesibles será verdadera la proposición condicional: 'si Miriam es el primer ser que sale al encuentro de Jefté entonces Jefté inmola a Miriam' ('∀y(Sy↔y=b)→Mab'). Esto implica que en todos los mundos accesibles en que es el caso que Miriam es el primer ser que sale al encuentro de Jefté también es el caso que Jefté la inmola. Dada la prohibición divina de inmolar a los hijos, los mundos en que Miriam es hija de Jefté y Jefté la inmola no son deónticamente accesibles. Por tanto, es posible que no haya ningún mundo deónticamente ideal al que Jefté pueda de hecho acceder, ya que no puede transformar las cosas de modo que Miriam no sea su hija o no sea el primer ser que salió a su encuentro. Pero esto sólo significa que, dadas las circunstancias, Jefté no puede de hecho cumplir con todas sus obligaciones, lo cual, como ya se vio, es distinto de sostener que éstas sean inconsistentes.

La interpretación semántica de la premisa (2) que se propuso anteriormente, de acuerdo con la cual en todos los mundos accesibles Jefté inmola a quien satisface la descripción, sólo es compatible con la concepción insular de las normas condicionales, pues las normas condicionales concebidas de acuerdo con la concepción puente no excluyen por sí mismas ningún mundo. En cambio, unidas a la proposición que afirma que Miriam es el primer ser que sale al encuentro de Jefté determina que Miriam sea inmolada por Jefté en todos los mundos accesibles.

La discusión precedente pretende poner de manifiesto que la concepción puente no permite distinguir conceptualmente entre tener una obligación de realizar actos de cierto tipo, digamos A —por ejemplo, matar a Miriam—, y tener una obligación tal que, dadas las circunstancias, sólo podría ser satisfecha haciendo actos de tipo A. sin embargo, la distinción es importante, ya que la adscripción de obligaciones es sensible a la forma en que se describe el contenido de tales obligaciones.

Supongamos, por ejemplo, que fuera verdad que es obligatorio maximizar el bienestar general y supongamos, asimismo, que, de hecho, en cierta oportunidad, los únicos actos óptimos desde el punto de vista de la promoción del bienestar general son de cierto tipo, por ejemplo, actos de gritar "¡viva la Patria!". De ello no se sigue que es obligatorio gritar "¡viva la Patria!". Sólo se sigue que la obligación de maximizar el bienestar general sería violada por los agentes que, en la ocasión de que se trata, omitieran gritar esa frase. En términos generales, que sea obligatorio un acto de tipo A y que, de hecho, todo acto de tipo A sea de tipo B y todo acto de tipo B sea de tipo A, no implica que sea obligatorio realizar un acto de tipo B. Para el razonamiento práctico esta implicación es innecesaria porque no es necesario invocar que el acto realizado es de tipo B, por ejemplo, gritar "¡viva la Patria!", para dar cuenta de las razones normativas que el agente tenía para llevarlo a cabo. Desde el punto de vista de la norma involucrada, la única propiedad relevante del acto realizado es A —en el ejemplo, que se trata de un acto que maximiza el bienestar general—, y la norma que hay que invocar para justificarlo es la que establece que se debe maximizar el bienestar general. En el caso de Jefté, la única norma que tiene que invocar para justificar la inmolación de Miriam es la que establece la obligatoriedad de inmolar al primer ser que salga a recibirlo. No necesita invocar, además, una norma que establezca la obligación de inmolar a Miriam y, por tanto, no hay ninguna razón para postular tal norma. Es que, si la invocación de normas tiene por objeto justificar acciones o suministrar razones a otro agente para que realice un acto, la propiedad relevante es que se trataba de un acto de inmolar al primer ser que había salido a su encuentro y la norma que hay que invocar es la que establece la obligación de inmolar a quien porta esa propiedad.

Las acciones individuales son susceptibles de diversas descripciones, y pueden tener propiedades que han sido calificadas normativamente de distinta manera. Eso no tiene por qué ser visto como una contradicción normativa. La maniobra de un conductor en una determinada ocasión puede ser a la vez un acto de girar a la derecha en una esquina determinada y un acto de encerrar a otro vehículo. Puede ocurrir que esté permitido girar a la derecha y prohibido encerrar vehículos. El inspector de tránsito podría decir al conductor, sin incurrir en contradicción: "no lo multo por el hecho de haber girado a la derecha sino por el hecho de haber encerrado a otro automóvil". El aparato lógico debería ser apto para mostrar esas distinciones. ¹⁶

Tercera observación:

Como ya señalé, la defensa de la concepción puente se debe a que ésta es necesaria para construir la fundamentación de las sentencias judiciales como un razonamiento deductivo, pues su estructura condicional es lo que permite la aplicación de la regla de separación o 'modus ponens'.

Ahora bien, la validez de la regla del modus ponens implica la validez de la ley de refuerzo del antecedente, como muestro a continuación.

La ley de refuerzo del antecedente consiste en la siguiente tautología: '(A→B)→((A∧C)→B)'. Su explicación intuitiva es la siguiente: El condicional material expresa que el antecedente es condición suficiente del consecuente. Si es verdad que A es condición suficiente de B, entonces, cuando se da A se da también B, tanto si se da concomitantemente cualquier otro hecho C como si no. Por ende, cuando es verdad 'A→B' también será verdadero el condicional '(A∧C)→B'. Ahora bien, supóngase que no valiera la ley de refuerzo del antecedente pero se aceptara la regla del modus ponens. Entonces, debería haber un caso en que 'A→B' es verdadera pero '(A∧C)→B' es falsa. Para que esto último ocurriera, la interpretación debería hacer verdadera a 'A∧C' y falsa 'B'. Pero si es verdadera 'A∧C', es verdadera 'A' —a menos que se interprete la conjunción en algún otro sentido— y, como estamos suponiendo la verdad de 'A→B', la regla del modus ponens nos permite inferir 'B'.¡Contradicción!

La ley de refuerzo del antecedente, unida a la concepción puente de las normas condicionales, tiene algunas consecuencias antiintuitivas:

Considérense dos normas condicionales cualesquiera que relacionan situaciones fácticas totalmente independientes con consecuencias normativas incompatibles, como por ejemplo: 'si está ventoso debe cerrar la ventana', esquematizable, de acuerdo con la concepción puente, como 'q→Or', y 'si hace calor puede no cerrar la ventana', cuyo esquema, siguiendo los mismos lineamientos, sería 's→P¬r'. La lógica proposicional permite derivar de ambas la siguiente norma: '(q∧s)→(Or∧P¬r)'. Por otro lado, para la lógica deóntica standard el consecuente de esta última norma es una contradicción, es decir que se puede derivar como teorema '¬(Or∧P¬r)'. De esto último, junto con la norma '(q∧s)→(Or∧P¬r)', se sigue, en virtud de la lógica proposicional (modus tollens), '¬(q∧s)' ¹⁷ . A la vez, de '¬(q∧s)' se puede deducir cualquier norma cuyo antecedente sea 'q∧s'; por ejemplo, '(q∧s)→Ot' (ex falso sequitur quodlibet). Asimismo, es fácil ver que de las normas 'q→Or' y 's→P¬r', junto con la premisa 'q', se deduce '¬s'. Es decir que de normas que contemplan circunstancias lógicamente independientes se puede deducir la imposibilidad de ciertos hechos cuya descripción no es contradictoria, y, además, otras normas a partir de esas afirmaciones de hecho. En suma, el puente que tiende esa concepción de las normas entre lo que es el caso y el reino del deber parece ser demasiado ancho.

V. Deducción y aplicación de normas

Discutiré aquí las razones invocadas para sostener la concepción puente de las normas condicionales.

La idea de Alchourrón parece ser que, si no pudiera usarse el modus ponens deóntico para deducir normas categóricas cuando se dan ciertas circunstancias de hecho, las normas condicionales serían totalmente inútiles, ya que ninguna consecuencia práctica podría derivarse de ellas. "¿Cuál es —se pregunta Alchourrón en el contexto de la discusión relativa a la derrotabilidad— el uso práctico de un condicional (o de una relación de consecuencia) que, de la verdad del antecedente (las premisas) no nos permite inferir la verdad del consecuente (la conclusión)?" [1993].

A mi modo de ver, es un error suponer que las mismas consideraciones que son aplicables a los enunciados condicionales descriptivos y al razonamiento especulativo tendiente a derivar ciertas proposiciones a partir de otras que se suponen verdaderas, serán también aplicables al razonamiento práctico que permite fundar en reglas generales las acciones y decisiones. ¹⁸ En este último caso, creo que simplemente no es verdad que las normas condicionales, concebidas de acuerdo con la concepción insular, tengan menos consecuencias prácticas que las normas puente.

Para probar este punto compararé las consecuencias prácticas de una norma puente, como 'p—Oq', con las de una norma insular formada con las mismas proposiciones, esto es, 'O(p—q)' ^19.

Si las normas son verdaderas en un mundo donde es verdad 'p', de la norma puente puede inferirse 'Oq', lo que significa que todos los mundos deónticamente accesibles serán mundos q. Por tanto, serán mundos p∧q o mundos ¬p∧q. Por su parte, la verdad de la norma insular consiste en que en todos los mundos accesibles es verdadero el condicional 'p→q'. Esto, a su vez, equivale a sostener que los mundos deónticamente accesibles son mundos p∧q o ¬p∧q o ¬p∧¬q. Como puede apreciarse, la única diferencia entre los tipos de mundos admitidos por ambas normas está en que la insular admite los mundos ¬p∧¬q, en tanto que la norma categórica derivada de la norma puente no los admite. Sin embargo, hemos supuesto que nos encontramos en un mundo p. Si de hecho no fuera posible transformarlo en un mundo ¬p, la única posibilidad real de ajustar la conducta a la norma parece ser en ambos casos la misma, a saber, hacer que el mundo sea p∧q, o, en caso de que ya sea p∧q, evitar que se transforme, o abstenerse de transformarlo, en un mundo p∧¬q. ²⁰

Supongamos ahora que nos encontramos en un mundo donde es verdad '¬p'. En ese mundo, la norma puente 'p→Oq' no excluye ningún mundo. todo mundo lógicamente posible puede ser deónticamente accesible. Por su parte, la norma insular determina en este caso los mismos mundos accesibles que en el mundo considerado anteriormente, ya que los hechos del mundo no la afectan. Por tanto, los únicos mundos accesibles son aquí también mundos p∧q o ¬p∧¬q o ¬p∧q. Como vemos, la norma insular también sirve para orientar la conducta cuando el mundo es ¬p porque, si no deseamos q, sabemos que podemos conseguir que el mundo real se siga pareciendo al ideal deóntico si evitamos que acaezca p. En cambio, la norma p→Oq no define ningún ideal deóntico en el mundo ¬p. Supongamos que p consiste en prometer dar una suma de dinero a alguien y q consiste en dársela. La norma O(p→q) nos obliga a no prometer a menos que cumplamos la promesa. La norma p→Oq no nos obliga a nada.

Supóngase ahora que la conducta q está prohibida por otra norma, es decir, que es verdad la norma categórica 'O¬q' y estamos en un mundo ¬p. La norma insular 'O(p→q)' junto con la norma categórica antedicha implican 'O¬p' —no debemos hacer aquello que nos compromete a hacer lo prohibido—. En cambio, la norma 'p→Oq' junto con O¬q no tiene ninguna consecuencia normativa relativa a p ²¹ .

Como puede apreciarse con estas simples consideraciones, la afirmación de que las normas condicionales no pueden tener consecuencias prácticas a menos que, en unión con ciertas proposiciones descriptivas, permitan deducir normas categóricas no es acertada. ²²

La idea de que la naturaleza de la justificación de las decisiones sobre la base de reglas es deductiva puede también ser atacada desde otro ángulo.

Un ejemplo paradigmático de actividad fundada en reglas es la que llevamos a cabo cuando justificamos cada paso de una deducción mediante la invocación de reglas de inferencia.

En efecto, desde un punto de vista sintáctico, que A es consecuencia deductiva de B significa que existe una secuencia finita de fórmulas que parte de B y culmina en A, y donde el agregado de cada fórmula se encuentra justificado por una regla de inferencia. Ahora bien, ¿qué significa la expresión 'se encuentra justificado' en este contexto? ¿Significa acaso que el contenido de la fórmula agregada se deduce de la regla de inferencia, junto con algunas proposiciones fácticas?

Las reglas de inferencia son enunciados del metalenguaje de estructura condicional, que establecen que, si en uno o más renglones de una deducción aparecen fórmulas de cierto tipo, se puede agregar en un nuevo renglón otra fórmula de cierto tipo. Por ejemplo, 'si en un renglón aparece una fórmula de tipo A→B y en otro renglón aparece A, se puede agregar B en un renglón subsiguiente' (regla de separación). Cuando introducimos en un renglón la fórmula B con fundamento en esa regla de inferencia, normalmente escribimos a un lado el nombre de la regla y los números de los renglones en que aparecen las fórmulas A→B y A, y nadie dudaría de que hemos justificado la introducción de B. Pero, ¿diríamos que esta justificación consiste en que la permisión de escribir B se deduce de la regla de inferencia, junto con el enunciado descriptivo que afirma que en un renglón está A→B y en otro renglón está A? Para poder justificar la afirmación de que 'se deduce' sería necesario invocar una regla de inferencia. Es decir que haría falta una metarregla de inferencia –formulada en el metametalenguaje– que estableciera que cuando se da una regla de inferencia y además se da en el lenguaje objeto la situación prevista en el antecedente de la regla, está permitido escribir la fórmula indicada en el consecuente de la regla. Ahora bien, de existir esa metarregla, podremos decir que se la ha utilizado para fundar la afirmación de que la permisión de escribir B se deduce de la regla de inferencia junto con el enunciado que afirma que en un renglón de la secuencia aparece la fórmula A→B y en otro, la fórmula A. Pero, ¿diremos que esa afirmación se deduce de la conjunción de la metarregla de inferencia con la regla de inferencia y el enunciado que afirma que aparecen las fórmulas A→B y A? Para poder sostener esto fundadamente sería necesario invocar una metametarregla de inferencia, formulada en el metametametalenguaje, que dijera ... Y así hasta el infinito.

Lo que ocurre en realidad es que cuando se invoca la regla de inferencia para justificar una deducción como la del anterior ejemplo, lo que se afirma es que B se deduce de A→B y A, no que se deduce de A→B, A y la regla de inferencia, ya que exigir ese requisito produciría un regreso al infinito. En otras palabras, la regla que justifica la deducción no es una premisa más.

Con este argumento pretendo mostrar que hay al menos un caso de uso de reglas en que la justificación del contenido de una decisión mediante la invocación de una regla no involucra el tipo de relación deductiva que postula la concepción deductivista. Pero si esto vale para las reglas de inferencia, no advierto por qué no habría de valer también para otros tipos de reglas.

VI. Conclusiones

He sostenido que la concepción deductivista de las sentencias judiciales, según la cual la exigencia de que las sentencias sean fundadas en derecho consiste en que el contenido de la decisión se deduzca de ciertas premisas normativas y fácticas, es errónea.

La tesis deductivista depende esencialmente de un análisis de la estructura lógica de las normas condicionales que me parece desacertado: la llamada 'concepción puente', que considera a las normas de ese tipo como enunciados condicionales mixtos, formados por un antecedente descriptivo y un consecuente normativo. He tratado de mostrar que la idea de que pueden deducirse normas a partir de la combinación de premisas normativas y fácticas presenta diversos inconvenientes y tiene algunas consecuencias absurdas.

La defensa de la concepción puente se debe a la creencia de que la concepción insular no permite justificar decisiones. Pretendo haber mostrado que esa creencia es errónea, ya que las normas concebidas de acuerdo con esta última concepción definen ideales deónticos que sirven como guías de conducta en situaciones en que la concepción puente no permite extraer consecuencia práctica alguna.

Por último, he mostrado que la idea de que la justificación de una decisión mediante la invocación de reglas requiere necesariamente que exista una relación deductiva entre la conclusión y ciertas premisas normativas y fácticas no podría ser sostenida de manera general, para todo tipo de decisiones basadas en reglas.

Referencias Bibliográficas

Alchourrón, Carlos E. (1993) "Philosophical Foundations of Deontic Logic and the Logic of Defeasible Conditionals", en Meyer, J.J. and Wieringa, R.J. (ed.), Deontic Logic in Computer Science: Normative System Specification, pp. 43-84, Wiley & Sons, 1993 .

Alchourrón, Carlos E. (1996 a) "On Law and Logic", Ratio Juris 9, vol. núm. 4, pp. 331-348. Las citas son de la versión en castellano: "Sobre derecho y lógica", Isonomía, núm. 13, pp. 11-33, 2000.

Alchourrón, Carlos E. (1996 b) "Detachment and defeasibility in deontic logic", Studia Logica 57, 5-18.

Alchourrón, Carlos E. y Bulygin, Eugenio (1971) Normative Systems, Springer-Verlag, Wien. Las citas son de la versión en castellano: Introducción a la metodología de las ciencias jurídicas y sociales, Astrea, Buenos Aires, 1974.

Anscombe, G.E.M. (1957) Intention, Basil Blackwell, Oxford. Reimpreso por Harvard Univiversity Press, Cambridge, Mass., 2000.

Åqvist, Lennart (1984) "Deontic Logic", en Gabbay, D. and Guenthner, F. (eds.) Handbook of Philosophical Logic, vol. II, pp. 605-714, D. Reidel, Holland.

Fallos: Fallos de la Corte Superma de Justicia de la Nación.

Hansson, Sven Ove and Makinson, David (1995) "Applying Normative Rules with Restraint", presentado en LMPS-95, Florencia, Italia, 19-25 de agosto de 1995.

Hintikka, Jaako (1971) "Some Main Problems of Deontic Logic", en Hilpinen, R. (ed.), Deontic Logic: Introductory and Systematic Readings, D. Reidel, Dordrecht, Holland, 1971, pp. 59-104.

Hughes G.E. y Cresswell, M.J. (1996) A New Introduction to Modal Logic, Routledge, London and New York.

Kripke, S.A. (1963) "Semantical Analysis of modal logic I, normal propositional calculi", Zeitschrift für mathematische Logik und Grundlagen der Mathematik, 9, pp. 67-96.

MacCormick, Neil (1978) Legal Reasoning and Legal Theory, clarendon Press, Oxford.

Rodríguez, Jorge L. (2002), Lógica de los sistemas jurídicos, Centro de Estudios Políticos y constitucionales, Madrid.

Schauer, Frederick (1991), Playing by the Rules. A Philosophical Examination of Rule-Based Decision-Making in Law and in Life, clarendon Press, Oxford.

Von Wright, Georg Η. (1951) "Deontic Logic", Mind, 60, pp. 1-15.

Von Wright, Georg Η. (1983) "On So-called Practical Inference", en von Wright, G.H., Practical Reason, Cornell Univ. Press, Ithaca, New York, 1983, pp. 18-34.

von Wright, Georg Η. (1984) "Bedingungsnormen - ein Prüfstein für die Normenlogik", en Krawietz, Werner (ed.) Theorie der Normen, Berlín, 1984.

Zuleta, Hugo R. (1999) "Análisis lógico-semántico de las normas jurídicas: las normas como contextos no extensionales en el razonamiento jurídico", Doxa (22), pp. 121/133.

Notas

¹ La conjunción de una, dos o más propiedades constituye lo que los autores denominan 'un caso genérico'. Las normas generales son pensadas como enunciados que correlacionan casos genéricos con soluciones normativas.

² Cabe aclarar que esta presentación de interpretaciones posibles no pretende ser exhaustiva.

³ Conviene aclarar que la calificación de una sentencia como arbitraria por no derivar de las normas del sistema tiene un sentido descriptivo, i.e. no conlleva necesariamente un juicio de valor negativo. Es más, podría considerarse conveniente y valioso que en algunas circunstancias los jueces resolvieran sobre la base de otro tipo de consideraciones. Es que, como ha explicado Schauer (1991), las reglas son generalmente sobreincluyentes y, a la vez, subincluyentes con relación a los fines que justificaron su creación, lo que hace que su aplicación estricta pueda parecer inconveniente en ciertos casos. Cuál sea el grado de libertad que deba acordarse a los jueces para apartarse de lo que disponen las normas generales, en aquellos supuestos en que su aplicación estricta aparece como opuesta a la finalidad para la que fueron creadas, es un problema de política judicial cuya solución podrá ser distinta según el contexto político en que se plantee. Asimismo, las expectativas sociales prevalecientes sobre el grado de apego a las reglas que deberían evidenciar los jueces pueden ser distintas en distintas sociedades y en distintos momentos de una misma sociedad. Lo que me interesa destacar es que, cualquiera sea la respuesta que se dé a esa pregunta, en nada afecta a la concepción deductivista de las sentencias, pues ésta no pretende ser un criterio de valoración sino de reconstrucción racional de la idea de fundamentación.

⁴ En Åqvist (1984) se lo denomina 'OK+' y en Hughes & Cresswell (1996), 'sistema D'. Åqvist llama 'lógica deóntica fuertemente normal de tipo von Wright (proposicional monádica)' a todo sistema que incluya a OK+.

⁵ Para una demostración puede verse Hughes & Cresswell (1996, pp. 39 y ss. y 119 y ss.).

⁶ Reconozco que es filosóficamente insatisfactorio atribuir valores de verdad a las normas. Sin embargo, ello es técnicamente posible, ya que la lógica deóntica es una extensión de la lógica proposicional, y resulta conveniente porque facilita enormemente el análisis. Por ese motivo es un procedimiento usual en lógica deóntica. Como es sabido, el principal problema de la lógica deóntica es su justificación, pues, si las normas carecen de valor de verdad, no parece claro qué quiere decir que una norma se sigue lógicamente de otra o que dos normas son contradictorias. Se han propuesto diversas soluciones, pero no las discutiré en este trabajo.

⁷ Las pruebas de adecuación y completitud del sistema D pueden verse en Hughes & Cresswell (1996, pp. 45 y 118-120).

⁸ Véase, por ejemplo, Hintikka (1971).

⁹ Adaptado a partir de un ejemplo de Hansson and Makinson (1995).

¹⁰ El uso de cuantificación es aquí indispensable, ya que las limitaciones expresivas de la lógica proposicional no permiten analizar adecuadamente el ejemplo. La mayoría de las lógicas deónticas se apoyan exclusivamente en la lógica proposicional, lo que les resta utilidad para el análisis formal de los más elementales razonamientos normativos que se formulan en el lenguaje ordinario. sin embargo, a los fines de los ejemplos que se tratan en este apartado, se puede emplear la lógica cuantificacional sin mayores aclaraciones, pues no plantea dificultades especiales, dado que la norma en consideración tiene la forma OA, cuyas condiciones de verdad ya fueron explicadas. Lo único novedoso es que la cuantificación permite extraer de la oración que ocupa el lugar de a consecuencias lógicas que no podríamos obtener si sólo pudiéramos valernos de la lógica proposicional.

¹¹ Omito la prueba en razón de su simplicidad. Se obtiene utilizando RNO, AKO y la regla de eliminación del condicional (modus ponens).

¹² Una acción genérica es una propiedad que una acción individual puede tener o no tener y que permite identificar a una acción individual como de un tipo determinado. Por ejemplo, matar, robar, violar, son acciones genéricas, que pueden ejemplificarse en diversas acciones individuales.

¹³ Por cierto, esta objeción pierde fuerza si se admite atribuir valores de verdad a las normas, como ocurre en este trabajo. sin embargo, la explicitación de condiciones de verdad en términos de mundos accesibles resulta problemática para las normas de la concepción puente, porque las condiciones son diferentes según cómo sea el mundo de referencia. En un mundo en que es verdad ¬p será verdadera toda norma cuyo antecedente sea p, sin importar cómo sean los mundos accesibles. En un mundo p, en cambio, las condiciones de verdad de esa norma coincidirán con las de la norma categórica que aparezca en su consecuente. Por tanto, utilizando el término 'significado' en un sentido extensional puede decirse que el significado de las normas puente cambia según sea el mundo en que rigen.

¹⁴ Por ejemplo, en Alchourrón (1996 b) dice: "In order to enter the deontic field the standard O operator of system D is added to the construction ... A sentence like OA will be intuitively interpreted as standing for the actual (indefeasible) duty to do A. so the notion of actual obligation is our primitive deontic concept". Adviértase que, si bien Alchourrón concibe la fórmula 'OA' como expresando un deber actual —por oposición a un deber condicional—, lo cierto es que las reglas de formación del sistema D no excluyen que la fórmula que aparece en el lugar de 'A' pueda tener cualquier forma, incluyendo, obviamente, la condicional.

¹⁵ En virtud de la regla conocida como 'ejemplificación universal' o 'eliminación de V en los métodos de deducción natural.

¹⁶ En otro trabajo (Zuleta, 1999) he señalado la importancia de la distinción entre hechos y acontecimientos. Allí sostuve que dos descripciones no se refieren al mismo hecho si no son lógicamente equivalentes, a diferencia de lo que pasa con los acontecimientos. También mostré la relevancia de la distinción para interpretar las normas tributarias.

¹⁷ Esto es tanto como decir que la verdad de ciertas normas hace que ciertas proposiciones no contradictorias resulten necesariamente falsas, pues ningún modelo puede hacerlas verdaderas en un mundo donde sean verdaderas tales normas.

¹⁸ Conforme señala von Wright (1983), puede distinguirse dos tipos de inferencia práctica: la que subsume una cosa o acción particular bajo cierto principio general o regla, y la que se utiliza como esquema de explicación o comprensión de las acciones intencionales por referencia a ciertos fines del agente. Aristóteles, que introdujo el concepto de 'silogismo práctico', lo usó en el primer sentido, según se desprende de los ejemplos que presentó. Según Anscombe (1957), el razonamiento práctico fue uno de los mejores descubrimientos de Aristóteles, pero su verdadero carácter ha sido oscurecido, ya que "comúnmente se supone que es una especie de razonamiento ordinario que lleva a una conclusión del tipo 'debo hacer tal y tal cosa'". Por 'razonamiento ordinario' entiende "el único tipo de razonamiento considerado generalmente en filosofía: el razonamiento hacia la verdad de una proposición, que es supuestamente mostrada por la verdad de las premisas". Sostiene la autora que explicar el razonamiento práctico como un tipo de razonamiento probatorio (deductivo) constituye una confusión en la que ha incurrido la mayoría de los filósofos.

¹⁹ Esto no significa que esté defendiendo la tesis de que el condicional material es una forma adecuada de representar las normas condicionales. Es sabido que esta idea fue inicialmente sostenida por von Wright, pero luego fue abandonada debido a las dificultades que presenta, especialmente con relación a la representación de obligaciones contrarias al deber, esto es, la imposibilidad de dar cuenta de la idea intuitivamente clara de que a veces hacer lo prohibido nos compromete a hacer alguna otra cosa. Por ejemplo, tenemos obligación de no dañar a otro, pero si lo dañamos, tenemos obligación de indemnizarlo. Esto ha llevado a muchos autores, entre ellos von Wright, a abandonar las lógicas deónticas monádicas a favor de las diádicas, que, en general, gozan actualmente de mayor aceptación. No hay, entonces, una sola manera de concebir las normas condicionales dentro de la llamada 'concepción insular'. in embargo, en este trabajo no necesito pronunciarme a favor de ninguna concepción en especial. Lo único relevante para mis propósitos es lo que todas tienen en común, es decir, que no validan el modus ponens deóntico.

²⁰ Para saber lo que tenemos que hacer en determinadas circunstancias, dadas ciertas normas generales, lo que necesitamos no es deducir una nueva norma, sino aplicar una regla técnica. No necesitamos agregar una norma categórica para justificar nuestra acción, sino señalar que existe una necesidad práctica de actuar de cierta manera para que el mundo se parezca al ideal deóntico. Una idea similar sostiene von Wright (1984).

²¹ La consecuencia que tiene es que p es imposible, lo cual es absurdo.

²² La generalidad de las variables proposicionales utilizadas deja abiertas muchas posibilidades. Podría ser que 'q' se refiriera a un estado de cosas que se produce en un momento posterior a aquél en que se produce p, de modo que, una vez acaecido p, la única manera de obtener un mundo deónticamente ideal es haciendo que q sea el caso. Podría ser que la realización de p dependiera del mismo agente de cuya acción depende la realización de q (es decir, el destinatario de la norma) o que dependiera de un tercero o que se tratara de un hecho de la naturaleza. La concepción puente parece considerar solamente aquellas situaciones en que, una vez que p es el caso, no hay manera de modificar ese hecho.

IR