Uno de los conceptos que aparecen como básicos en la descripción del derecho como un sistema dinámico es el de derogación. El objeto de este trabajo es el tratar de tomar en consideración algunos aspectos de la derogación normativa, que creo deben tenerse en cuenta en los análisis que se hacen acerca de la derogación a partir de la lógica jurídica. ¹ En este sentido, quienes por primera vez hicieron notar las peculiaridades y los problemas lógicos derivados de la derogación de normas han sido Alchourrón y Bulygin. ²

Para comenzar, debo decir que aceptaré la idea de estos autores conforme a la cual las consecuencias lógicas de las normas deben ser consideradas normas del sistema, por lo que habrá normas no formuladas sino derivadas que forman parte del sistema. ³ También entenderemos por “sistema jurídico” un conjunto de normas válido en cierto momento de conformidad con algunos criterios de pertenencia, y por “orden jurídico” una secuencia de sistemas normativos. Es decir que un sistema jurídico es momentáneo y cambia cada vez que se cambia una norma de éste. El orden jurídico, en cambio, se extiende en el tiempo, y en él se agregan o derogan normas sin que deje de ser el mismo. ⁴ Dos sistemas son diferentes cuando contienen normas distintas.

En la derogación de normas, juega un papel fundamental el criterio lex posterior, ya que la sustitución de un sistema por otro en el orden jurídico se produce cuando una nueva norma sancionada deroga en forma expresa o tácita ⁵ alguna de las pertenecientes al sistema, con lo cual aparece otro sistema. Los criterios lex superior . lex specialis, aún cuando sirven para establecer preferencias entre normas incompatibles, ⁶ no suelen considerarse como productores de la derogación de normas si no operan junto con el de ley posterior. La derogación priva de validez, en el sentido de pertenencia al sistema, ⁷ a las normas afectadas por ella, por lo que no forman parte de los sistemas subsiguientes.

En el presente trabajo tendré en cuenta solamente la derogación de normas generales por otras normas con las mismas características. A veces se menciona como derogación la declaración de inconstitucionalidad que realizan los jueces, en un sistema de control difuso de constitucionalidad, como el que rige en mi país (en un sistema de control centralizado de constitucionalidad, con un Tribunal Constitucional ú otro similar, suele darse a éste la facultad de derogar efectivamente las leyes inconstitucionales. En este aspecto funciona como el poder legislativo cuando deroga expresamente una norma). Se suele decir, en sistemas como el nuestro, que una norma declarada inconstitucional es derogada respecto del caso. En este supuesto se trata de privar a una norma de validez, en el sentido de aplicabilidad. En general, en los sistemas de control difuso, la norma sigue perteneciendo al sistema, por lo que no se encuentra derogada, en el sentido que estamos tratando aquí.

Para que haya derogación, debe haber una norma preexistente. En general no se dice que la constitución, p. ej. deroga a las futuras leyes inconstitucionales. El criterio jerárquico, lex superior, es utilizado para derogar normas cuando se introduce una norma superior incompatible con una norma inferior que formaba parte del sistema. El análisis formal respecto de la derogación será, en este caso, idéntico al de la introducción de una norma posterior de la misma jerarquía. Tampoco se dice que una ley anterior especial deroga a una posterior general (me referiré más extensamente al criterio de lex specialis más abajo). Sin embargo, la operación conceptual es en todos los casos idéntica: en un conjunto de normas que se acepta como válido aparecen dos normas total o parcialmente incompatibles, y, descartada la eliminación mutua, debe establecerse un criterio de selección para eliminar alguna y preservar la consistencia del sistema.

La derogación puede ser expresa . tácita. Mediante la primera se elimina la formulación de una norma que pertenece a un sistema jurídico, de modo que no aparece en los sistemas sucesivos, por medio de un acto de derogación. La derogación tácita resulta más compleja, ya que se produce mediante la sanción de una norma que regula el mismo caso genérico con un contenido incompatible. ⁸ Aquí lo que hay es un acto de promulgación de una norma, y como la agregación de esta norma torna al sistema en inconsistente, se restablece la coherencia mediante la derogación de la norma preexistente, aplicando el principio de lex posterior. Por lo tanto, solo en caso de derogación expresa se puede hablar en sentido propio de la existencia de un acto de derogación.

En caso de derogación tácita, dos formulaciones normativas provenientes de una fuente aceptada, se interpretan como normas incompatibles, que conducen a una incompatibilidad formal. El intérprete muchas veces buscará, a través de máximas o principios interpretativos ú otros recursos semánticos, eliminar la incompatibilidad. La derogación tácita de una norma se presenta cuando el intérprete adopta la interpretación que concluye en que ambas normas son lógicamente incompatibles, y aplica el principio lex posterior, sólo o sumado a alguno de los otros. ⁹

Es importante analizar la concepción de la derogación de Alchourrón y Bulygin, en cuanto a la indeterminación del sistema resultante de la derogación de una norma derivada, ya que ello nos permitirá avanzar en la conceptualización de la derogación parcial.

I. Algunos ejemplos problemáticos

En la versión más explícita, ¹⁰ el ejemplo es: “En el sistema consistente de las normas 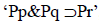, ‘Op’ y ‘Oq’, ha de ser derogada la norma ‘Pq’, por ejemplo el legislador dicta una norma declarando que la acción q no ha de considerarse como permitida...”. Sostienen los autores que en este caso la derogación de “Pq”, que se infiere de ”Oq”, lleva implícita la derogación de “Oq”, ya que no puede existir en el nuevo sistema una norma de la cual se deriva la derogada, y también la de “Pr”, que se infiere de las tres normas citadas, a través de Pp, derivada de Op y Pq. ¹¹

Continúan, en un nuevo ejemplo, diciendo: “Supongamos que en el sistema anterior se quiere derogar la norma ‘Pp&Pq‘. La derogación de esta norma implica la derogación de la norma ‘Pr’ que deriva de ella. Pero, ¿qué ocurre con las normas ‘Op‘ y ‘Oq’? es evidente que por lo menos una de estas normas debe desaparecer, pero la pregunta es ¿cuál de ellas? No hay criterios lógicos para decidir esta cuestión; se trata de un problema insoluble. El resultado de la derogación de la norma ‘Pp&Pq’ es, por lo tanto, no un sistema normativo, sino, por lo menos dos sistemas alternativos...” (que representan en diagramas, en uno de los cuales lo que se deroga es “Op”, y en el otro “Oq”.) También este tipo de derogación aparece con frecuencia en la práctica legislativa. El ejemplo típico y más corriente es la cláusula que suele insertarse al final de una ley, declarando que «quedan derogadas todas las disposiciones que se oponen a la presente..» Tal disposición puede, sin embargo, destruir la unidad del sistema, fracturándolo en diversas alternativas....El último caso analizado (derogación de una norma derivada) demuestra claramente que las dos operaciones –creación y derogación de las normas– no son simétricas. Nada análogo a la indeterminación lógica del sistema puede producirse al crearse una nueva norma. En lo sucesivo vamos a usar la expresión «indeterminación lógica del sistema normativo» como término técnico para caracterizar la situación en la que en lugar de un sistema aparecen varios sistemas alternativos.» ¹²

El problema es que se conceptualiza la derogación como una operación única, que sustrae de un conjunto de normas a la norma derogada. Cuando se trata de una norma formulada, la operación se puede hacer por la vía de mencionarla expresamente (derógase el art...) o mediante la sustitución por otra norma, lo cual a veces puede acarrear el problema de la derogación parcial, que trataré mas abajo.

Pero en el caso de una norma derivada, solamente se puede efectuar una derogación mediante una norma que sustituye a la derivada, ya que no se puede mencionar expresamente, p. ej. el número de artículo de la ley. Esto es lo que expresan Alchourrón y Bulygin en la frase subrayada mas arriba. “Pq” se sustituye por una norma: “Phq”. Si trasladamos esto a la derogación de Pp&Pq, se verá que hay tres formas en que esta norma puede quedar derogada. En el sistema pueden aparecer, sancionadas por el legislador: Php&Pq; Pp&Phq y Php&Phq (si lo que se busca es prohibir q, solamente las dos últimas). ¹³ Pero entonces no hay indeterminación alguna. En el primer caso, la prohibición de p implica la derogación de Op, en el segundo la prohibición de q la de Oq, y en el último la de las dos, y todas implican la derogación de Pr. Sucede que el legislador puede optar por una formulación u otra, pero, una vez adoptada, no hay indeterminación. ¹⁴

La cláusula: «derógase toda norma que se oponga a la presente» no cumple ningún papel en cuanto a la indeterminación surgida de la derogación de normas derivadas. Como se ve más arriba, éstas solo pueden considerarse derogadas mediante la sanción de una norma incompatible expresa. ¹⁵ Puede sí, generar incertidumbre desde el punto de vista semántico, ya que es necesario interpretar las formulaciones normativas para saber qué normas resultan afectadas. ¹⁶

Me parece que el problema surge por la idea de concebir a la derogación como una operación idéntica en todos los casos, sin tener en cuenta si se realiza en forma expresa o mediante una nueva formulación normativa. Esto se verá más claro en el caso de derogación parcial, como se dirá mas abajo.

Otros ejemplos suscitan otras complicaciones.

II. Las complicadas correlatividades

En un trabajo de Bulygin ¹⁷ se plantea el siguiente ejemplo: Supongamos un reglamento de Facultad, que expresa: N1: los alumnos que están en condiciones de rendir Sociología, pueden rendir Filosofía del Derecho, N2: Los alumnos que han completado el tercer año pueden rendir Sociología; N3: Los alumnos que hayan completado el tercer año pueden rendir Internacional Privado. De estas tres normas se infiere que los alumnos de cuarto año pueden rendir tres materias, Sociología, Filosofía e Internacional Privado. Bulygin supone que se agrega una nueva norma N4: Ningún alumno podrá rendir Filosofía del Derecho e Internacional Privado en el mismo turno de exámenes. Derógase toda norma que se opone a la presente resolución. ¹⁸

La pregunta que se hace Bulygin es: ¿qué normas han quedado derogadas?, y responde que no puede subsistir el conjunto formado por N1, N2 y N3, por lo que alguna de las tres normas han quedado derogadas. Pero como no hay un criterio que permita elegir cuál, y la derogación de una u otra lleva a consecuencias distintas, aparece la indeterminación lógica.

Creo que el ejemplo es erróneo, y esto se ve si formalizamos el caso, a través de la lógica deóntica standard. Veamos qué normas se pueden inferir a partir de las dadas. Comencemos por las normas formuladas:

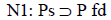
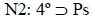
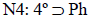(fd & ip) (salteo el paso obvio de «todos los alumnos» a «los alumnos de cuarto año»)

Se puede inferir:

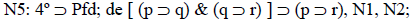
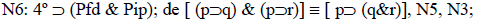
Pero comparemos N6 y N4. Para que N4 derogue N6 habría que inferir de N6 una N7: P (fd&ip). Sin embargo, esta no es una inferencia válida. De (Pp&Pq) no se puede derivar P (p&q). ¹⁹ De que dos conductas estén particularmente permitidas, no se puede derivar que la conjunción de ambas esté permitida. Un ejemplo sencillo: Contraer matrimonio puede estar permitido, y mantener relaciones sexuales con quien no es el propio cónyuge también puede estarlo, pero la conjunción de ambas conductas puede estar prohibida, en algunos sistemas jurídicos hasta constituir delito de adulterio. Si un sistema prohibe el adulterio, ¿alguien diría que se ha producido una indeterminación lógica, de modo tal que no se sabe si se derogó la norma que permite el matrimonio o la que permite tener relaciones sexuales con alguien que no sea el propio cónyuge? Al contrario, se dirá que ambas conductas siguen siendo permitidas, p. ej. para los solteros, pero lo que se prohibió es la conjunción de ambas. Otro ejemplo sería: conducir un automóvil y tomarse una botella de vodka son conductas individualmente permitidas, pero está prohibido conducir un automóvil habiéndose ingerido una botella de vodka. ²⁰

Otro tanto sucede en el ejemplo de Bulygin. N4 no ha derogado N6, tanto que cualquier alumno podría rendir Filosofía o Internacional Privado (pero no las dos) sin infringir ninguna norma, ya que esas conductas siguen siendo permitidas. No se ha derogado ninguna norma derivada, y por lo tanto, no hay indeterminación lógica alguna.

III. Indeterminaciones genuinas y derogación mínima. La conservación de las especies

Buscando otros ejemplos, encuentro uno diseñado sobre el patrón de los de Alchourrón y Bulygin en un trabajo de Orunesu, Rodríguez y Sucar. ²¹ Suponen éstos autores un sistema en el cual se encuentren las siguientes normas: N1: «Está permitido conservar las piezas de caza de los animales cuya caza está permitida»; N2: Es obligatorio cazar a la especie x». De N2 se infiere N3: «Está permitido cazar a la especie x», y de N3 y N1, N4: «Está permitido conservar las piezas de caza de la especie x».

Luego los autores dicen: «Supóngase finalmente que el legislador deroga la norma N4, esto es, aquella que establece que está permitido conservar las piezas de la especie de caza de la especie animal declarada plaga nacional. Aquí también se trata de la derogación de una norma derivada, pero dicha norma no se sigue solo de N1 ni de N4 sino de la conjunción entre ambas. En el sistema que resulte de esta derogación no deberá estar presente la norma expresamente derogada (en el caso N4) ni sus consecuencias lógicas. No obstante, ello no es suficiente: Si en el nuevo sistema subsistieran las normas N1 y N2, seguiría derivándose de ellas N4. Por consiguiente, algo más debe ser eliminado del nuevo sistema. Pero como la norma que aquí se quiere derogar es una consecuencia lógica, no de una, sino de dos o más normas formuladas, una de estas últimas deberá ser eliminada. Ahora bien, no hay ningún criterio lógico que indique cuál ha de desecharse. El resultado de esta operación será, por consiguiente, no un sistema sino un conjunto de sistemas alternativos: puede lograrse la eliminación de N4, sea eliminando N2 (y en consecuencia, también N3), o bien eliminando N1.» ²² Acto seguido introducen la noción de indeterminación lógica en forma idéntica a Alchourrón y Bulygin.

Sin embargo, creo que aquí aparece un problema derivado nuevamente de considerar a la derogación como una operación idéntica en todos los casos. Me parece que hay que dar cuenta desde el punto de vista lógico de la derogación parcial de normas, dado que, en caso contrario, se puede incurrir en alguna conclusión paradójica. Con esto no se introduce ningún concepto extraño a la práctica jurídica, ya que los legisladores suelen derogar parcialmente normas en forma expresa, utilizando fórmulas como: «derógase respecto de x la norma N...» o «derógase el último párrafo del art.....», y también puede producirse una derogación parcial en forma tácita, al oponerse una norma posterior de igual o mayor jerarquía o especialidad, parcialmente a una anterior. Este es siempre el caso cuando opera el principio de lex specialis.

Pensemos en el caso planteado por los autores mencionados. Una forma de solucionar la indeterminación en el sistema sería pensar en qué conclusión se derivaría de un sistema normativo que contuviera, para empezar, una N1 idéntica. Supongamos que en el lugar donde rige esa norma, se desata una molesta plaga de rinocerontes, y el legislador sanciona N2: «Es obligatorio cazar rinocerontes». De ésta se infiere N3: «está permitido cazar rinocerontes», y de ambas: N4: «está permitido conservar los rinocerontes cazados». Supóngase que se descubre que los cadáveres de rinocerontes transmiten enfermedades, y el legislador dicta N5: «está prohibido conservar los rinocerontes cazados».

¿Qué inferencia haría un jurista cualquiera? Que N5 deroga N1, o que N5 deroga N2, o ambas? Es obvio que no. Lo que diría es que N5 derogó parcialmente N1, es decir, derogó la permisión de conservar rinocerontes, pero sigue rigiendo para las demás piezas de caza. Tampoco diría que derogó N3, dejando de hacer obligatoria la caza de rinocerontes.

El problema surge de pensar que al derogar alguna consecuencia lógica de una norma se deroga ésta, o, en caso de indeterminación lógica, debe derogarse totalmente alguna de las normas involucradas. Si adoptamos el criterio de creer que toda vez que se deroga la consecuencia lógica de una norma se deroga ésta, obtenemos resultados curiosos.

En efecto, pensemos en un sistema S que posee una norma de clausura que permite en forma fuerte todas las conductas no prohibidas. Supongamos que en S hay una conducta “p” que no está prohibida. Por ende, como consecuencia lógica del sistema, se puede derivar “Pp”, como norma perteneciente a S. Si el legislador sanciona una norma: “Php”, ¿diremos que derogó la norma de clausura, transformando S en S1, un sistema incompleto? ¿O diremos que el sistema se transformó en S2, que incluye a la norma de clausura y Php, aunque ya no Pp?

Si nuestra lógica no permite dar cuenta de la derogación parcial, tendremos que aceptar sólo la primera conclusión. Pero esto eliminaría la posibilidad de considerar que una norma de clausura pertenece a un orden jurídico, y por lo tanto a sistemas posteriores, cuando se prohíbe alguna conducta que estaba genéricamente permitida.

Se puede admitir que se derogó parcialmente la norma de clausura, en el sentido de que una norma que antes se derivaba de ella ahora no puede inferirse, pero dejando como perteneciente al sistema a la misma y todas sus consecuencias lógicas, salvo la derogada (y las que se deriven de ella).

Habría que distinguir entre la derogación total, que implica eliminar de los sistemas subsiguientes la norma y sus consecuencias lógicas, de la derogación parcial, que sería la anterior.

Obviamente, si lo que se deroga es una norma formulada, se deroga totalmente. Pero nada impide admitir la derogación de parte de una norma o sólo alguna consecuencia.

El problema aparece cuando la derogación no es explícita, sino que, como se dice más arriba, se establece a través de la sanción de una norma incompatible con otra que forma parte del sistema. Aquí es inevitable recurrir a la caracterización lógica de la inconsistencia normativa. Pero ya Ross advertía que la inconsistencia puede no ser total sino parcial. ²³

Esto se da, en términos de Alchourrón y Bulygin, ²⁴ cuando se sanciona una norma que soluciona un caso más fino que el que estaba solucionado en el sistema, con una solución incompatible con la estatuida. Como se considera que una solución (modalización deóntica de una conducta) ²⁵ soluciona todos los casos más finos que el expresamente solucionado, aparece una contradicción normativa, que se resuelve acudiendo al principio lex posterior.

En el ejemplo: El caso caracterizado por las propiedades (simplificadas) A (animal) y PC (que está permitido cazar), aparece solucionado por la solución Pc (permitido conservar las piezas), de acuerdo con la norma 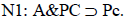. Si se agrega la propiedad R (rinocerontes), el caso A&PC&R también merece la misma solución: 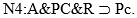. Por otra parte, hay una norma 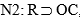, de la cual se infiere 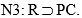. Pero el legislador introduce la norma . Si hay una incompatibilidad normativa es con N4, que, ciertamente, es una norma derivada de N1 (y de N2). Empero, esto no autorizaría a decir que N1 ha sido derogada en su totalidad. Al introducir la propiedad R, el legislador creó dos nuevos casos: 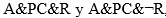, y solucionó mediante N5 solo el primero. El caso A&PC& ¬R sigue siendo solucionado por N1 (ya que es un caso más fino que A&PC).

En este caso –y no en los anteriores– se puede mencionar la existencia de una indeterminación lógica. Por cierto, se puede lograr la consistencia del sistema subsiguiente a la introducción de N5 tanto eliminando N2 como considerando que N1 ha sido derogada parcialmente. Empero, aquí se puede aplicar el principio de minimización cuantitativa, ²⁶ como condición racional de adecuación para la derogación. Mediante éste, los cambios realizados en el sistema a partir de la derogación de una norma derivada deben ser los mínimos necesarios. Así como no podría afirmarse que N5 derogó tanto a N1 como N2, por la aplicación de este principio, tampoco puede decirse que derogó a N2, ya que, al admitirse la derogación parcial de N1, basta con este cambio mínimo para la obtención de un sistema consistente.

IV. Vender o regalar

Veamos otro ejemplo. Supongamos dos normas:

N1: Los contratos que impliquen la transferencia de propiedad sobre inmuebles deben realizarse por escritura pública.

N2: El contrato de compraventa de inmuebles transfiere la propiedad sobre éstos.

De éstas se infiere

N3: El contrato de compraventa de inmuebles debe realizarse por escritura pública.

Supongamos que el legislador decide liberalizar los requisitos de la compraventa y sanciona

N4: El contrato de compraventa de inmuebles puede realizarse por instrumento privado.

En fórmulas:

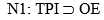
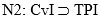
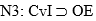
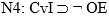
Es obvio que N4 ha derogado N3. Por lo tanto N3 no aparece en el nuevo sistema. Pero como N3 se infiere a partir de N1 y N2, debe considerarse que ha habido una derogación de alguna de las normas formuladas. Nuestras intuiciones jurídicas no nos permitirían sostener que ha sido derogada N2 o la totalidad de N1. Baste pensar que lo primero llevaría a desechar uno de los rasgos fundamentales de la compraventa, y lo segundo a sostener que la transferencia de la propiedad de un inmueble por medio de una donación, p. ej., no debe ser hecha por medio de escritura pública.

Acudiendo nuevamente a la minimización cuantitativa, podemos pensar que N1 se ha desdoblado en N5: 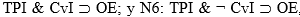, esto último conforme lo dicho mas arriba. Y N4 derogó sólo a N5, con lo cual esta última pertenece al nuevo sistema.

V. El trabajo y el alcohol

En otro trabajo, Bulygin ²⁷ adapta un ejemplo de Hilpinen para demostrar que hay casos de derogación «infelices», que llevan a una indeterminación.

El ejemplo es el siguiente: Consideremos dos normas: N1: Juan debe trabajar todos los días de la semana entre las 10 y las 18 hs.; N2: Juan no debe tomar alcohol mientras trabaja. Si quien dictó las normas agrega otra que dice: N3: Juan puede tomar alcohol los Sábados entre las 10 y las 18 hs., N3 es compatible tanto con N1 como con N2, pero no con la conjunción de ambas. Por ende, N3 debe haber derogado parcialmente alguna de las dos normas, permitiendo a Juan que no trabaje los Sábados o que los Sábados tome alcohol mientras trabaja.

Formalizando, en forma simplificada, las propiedades del caso son: D (días), H (horario de 10 a 18), T (trabajar), S (Sábados, y la acción considerada A (tomar alcohol)). Con el mismo análisis anterior tenemos:

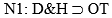
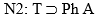
Aquí aparecen dos casos más finos que en N1: (D&H&S) y (D&H&¬S). Se puede interpretar que N3 solucionó el primero, y por lo tanto derogó parcialmente N1 (que se desdoblaría en 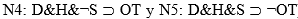), o, alternativamente N2 (que también se desdoblaría en 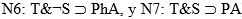). La introducción de N3 es compatible tanto con el sistema formado por N2, N4 y N5 como con N1, N6 y N7).

Pero aquí no se puede aplicar el principio de minimización cuantitativa, ya que en ambos casos hay que recurrir a una derogación parcial, y no se puede hablar de un caso como especial respecto de otro. ²⁸ Resultaría un caso irreductible de indeterminación lógica, que no se puede salvar mediante el criterio de minimización por el mismo motivo citado.

Digamos que en general se solucionará mediante la interpretación, acudiendo p. ej. A la intención del legislador ú otros principios no rigurosos.

VI. Derogación total y parcial

De acuerdo con lo expresado, se pueden clasificar distintas formas de la derogación.

1. a) Derogación total: A su vez, se puede dividir en a’) Expresa: Se deroga totalmente una norma de la base del sistema, mencionándola (p. ej.: “derógase el art... de la ley..,”; a») Tácita: Se deroga totalmente una norma de la base, o una derivada, mediante la introducción de una norma incompatible (p.ej.: Si en el sistema aparece legislada, o se deriva “Pp”, y se agrega “O¬p”).

   b) Derogación parcial: También se puede dividir en b’) Expresa: Se deroga parcialmente una norma de la base del sistema, también mencionándola (p.ej.: “derógase el segundo párrafo del art....”); b») Tácita: Se deroga parcialmente una norma expresa o derivada, mediante la introducción de una norma que solucione en forma incompatible un caso más fino que el que se hallaba contemplado en éstas.

   (p. ej. los casos expuestos en III y IV).

VII. Minimización cuantitativa y lex specialis

En la derogación parcial, como se ve, después del principio de lex posterior, juegan un papel importante el principio de minimización cuantitativa, y el principio de lex specialis.

Un caso genérico puede ser considerado especial respecto de un caso general, cuando es un caso más fino que éste, es decir, cuando comparte las mismas propiedades relevantes pero se le agrega una nueva propiedad, cuya presencia o ausencia es solucionada en forma incompatible con la solución deóntica dada al caso general.

Para establecer que ha habido una derogación parcial, se debe interpretar que la nueva norma ha introducido una propiedad que deriva en un par de nuevos casos, uno de los cuales aparece solucionado por la norma que se agrega en forma incompatible con la solución derivada del sistema anterior, y se transforma en un caso especial.

En este sentido, en los ejemplos anteriores, tanto la norma que prohíbe conservar los rinocerontes cazados, como la que permite la compraventa de inmuebles sin escritura, pueden ser vistas como una norma especial, que deroga parcialmente una norma general, la cual mantiene su validez en los casos que no coincidan con aquellos que regulaba la parte de la norma que resulta derogada.

El principio de minimización cuantitativa y el de ley especial se hallan íntimamente relacionados, aunque no son idénticos. El primero puede ser visto como la fijación de una restricción al segundo, y se ve reflejado, en la práctica jurídica, en la máxima interpretativa que expresa que las excepciones deben interpretarse en forma restrictiva.

Ninguno de los dos es un principio lógico, ²⁹ e involucran acudir a razones sustanciales, no formales, con lo cual sigue en pie la indeterminación lógica sustentada. Pero hay que tener en cuenta que lex posterior, que se presupone cuando se define la derogación, tampoco es un principio lógico. ³⁰ En todos los casos se trata de criterios de preferencia entre normas incompatibles, que permiten mantener la consistencia del sistema.

VIII. Conclusión

De lo dicho se infiere que si bien el fenómeno de la derogación puede llevar a la indeterminación lógica, a veces ella es solo aparente. En la consideración de un sistema jurídico, debe tenerse en cuenta la diferencia entre la derogación expresa y tácita, y, respecto de esta última, es importante distinguir entre la derogación total y la derogación parcial.

La derogación parcial puede analizarse lógicamente como la solución de un caso más fino que el que aparece en una norma con una solución deóntica incompatible con la de ésta.

En la operación de derogación parcial tácita se suele recurrir al principio de minimización cuantitativa, que, por otra parte, puede solucionar algunos casos de indeterminación, salvo que la introducción de una nueva norma lleve a la posible alternativa entre la derogación parcial de dos normas.

Notas

¹ Parte de las ideas expuestas en el presente trabajo fueron expuestas, bajo el mismo título, en las XVII Jornadas de Filosofía Jurídica y Social, organizadas por la Asociación Argentina de Filosofía del Derecho en la ciudad de Córdoba, del 24 al 26 de octubre de 2003. Allí recibieron los embates de Bulygin, y fueron objeto de otras observaciones, como las de Navarro o Guibourg. Agradezco todas las intervenciones, que me han ayudado a perfilar mejor el tema, aunque, en lo sustancial mi conclusión no ha variado. La insistencia es una virtud si uno acierta y un demérito si persiste en el error. Espero que sea el caso de lo primero.

² Ver “Sobre el concepto de orden jurídico”, en Análisis lógico y Derecho, Centro de Estudios Constitucionales, Madrid, 1991, págs. 393 y ss.

³ Jorge Rodríguez, a quien agradezco por haber leído una primera versión de este trabajo, y haberme formulado varias lúcidas críticas, algunas de las cuales me han servido para modificarlo, sin que, obviamente, pueda hacérselo responsable de las ideas que expongo, me ha remitido un trabajo intitulado “Las consecuencias lógicas de las normas jurídicas”, en el cual concluye en que una óptica positivista frente al derecho no necesita rechazar que las consecuencias lógicas de las normas pertenezcan al sistema jurídico, pero no es necesario clausurar el sistema jurídico mediante la noción de consecuencia lógica, con lo que las consecuencias lógicas de las normas de base (promulgadas) no serían parte del sistema. Discutir este punto me llevaría demasiado lejos. De todos modos, Rodríguez sostiene que debe asignare relevancia a las consecuencias lógicas de las normas, y que la operación de derogación posee iguales características se clausure el sistema mediante la noción de consecuencia lógica o no, con lo cual la discusión deja de ser importante para lo que se sostiene en el presente.

⁴ Se trata, por cierto, de definiciones estipulativas (ver Bulygin, Eugenio,“Tiempo y validez”, en Alchourrón, Carlos y Bulygin, Eugenio, Análisis Lógico y Derecho, Madrid, Centro de Estudios Constitucionales, 1991, p. 197), es decir que estipulan un significado, y no recogen el uso común de un término. Entre los juristas no hay un uso común aceptado. Las expresiones “orden jurídico” y “sistema jurídico” pueden llegar desde ser sinónimas hasta significar lo inverso a lo que se cita en el texto, o cosas diferentes.

⁵ Ver Aguiló Regla, Josep, “Derogación”, en Enciclopedia Iberoamericana de Filosofía, El Derecho y la Justicia, p. 200

⁶ Ver Guarinoni, Ricardo, Después, más alto y excepcional, Criterios de solución de incompatibilidades normativas, en Doxa, 24 (2001), Alicante, España, p. 547 y ss. .

⁷ La palabra “validez” es ambigua, y alude por lo menos a tres significados que cabe distinguir: como pertenencia al sistema de una norma, como aplicabilidad, y como obligatoriedad. (ver Bulygin, op. y loc. cit.)

⁸ Guastini, Riccardo, Distinguiendo, Gedisa, Barcelona, 1999, p. 373.

⁹ Ver Guarinoni, Ricardo, op. cit., p. 549

¹⁰ Sobre el concepto de orden jurídico, en Análisis Lógico y Derecho, cit., p. 401.

¹¹ La derivación se obtiene a través de la ley de subalternación deóntica: .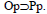

¹² Alchourrón y Bulygin, op. cit., págs. 402/3

¹³ Es obvio que para derogar una norma permisiva se debe sancionar una prohibición. “Derógase toda norma que permita q”no tiene sentido, salvo que en otra parte del sistema haya una norma que prohíba q o la clase de conductas de la cual forma parte, y del sistema se extrajera “Pq”, como excepción. En caso contrario, se tornaría necesario sancionar una norma “Phq”. Si un legislador optara por una formulación como la primera, con el carácter P u otro, podría plantearse la duda de si estamos ante una derogación expresa o tácita. Me inclino por clasificarla como tácita, a pesar de incluir un acto de derogación, ya que requiere de una operación posterior para determinar cuáles son las normas que serán eliminadas del sistema, máxime cuando pueden ser normas derivadas. Si el sistema contiene una norma de clausura que permite las conductas no prohibidas, y no contiene Phq, “derógase toda norma que permita q” derogaría parcialmente esta norma de clausura, pero habría una laguna respecto de q.

¹⁴ En una comunicación personal, criticando esta parte del trabajo, Eugenio Bulygin me sugiere que hay indeterminación lógica porque el legislador puede optar por cualquiera de las tres variantes reseñadas. Sin embargo, esto contradice el concepto citado de indeterminación, que se produce después de la sanción de una norma cuyo contenido no permite saber cuál de las normas ha quedado derogada.

¹⁵ En realidad, también puede darse el caso en que la derogación de una norma derivada, o expresa, provenga de una norma incompatible derivada de una norma promulgada. Omitiré considerar estos casos, que merecen consideración, para no complicar más el modelo.

¹⁶ Aguiló Regla, op. cit. p. 200, destaca que las cláusulas derogatorias genéricas del tipo de la expresada son redundantes respecto del principio de lex posterior, ya que si se acepta éste, las normas anteriores incompatibles con las sancionadas posteriormente quedan derogadas.

¹⁷ “Teoría y técnica de legislación”, en Análisis Lógico y Derecho, cit., p. 422. He modificado los subíndices de las normas para hacer más claro el ejemplo.

¹⁸ Bulygin no lo dice, pero se supone que hay un turno de exámenes por año, ya que en caso contrario podría interpretarse que no hay incompatibilidad entre N4 y las demás.

¹⁹ Ver p. ej. Echave, Urquijo y Guibourg, Lógica, proposición y norma, p. 142.

²⁰ En el texto citado en la nota anterior se demuestra que, a la inversa, 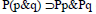es una ley de la lógica deóntica . Admitir la inferencia cuestionada significaría que P (p&q) y Pp&Pq se transformarían en fórmulas equivalentes. Por otra parte, aún cuando adoptáramos las ideas expuestas por von Wright en Norms, Truth and Logic (von Wright, Georg, Practical Reason, Philosophical papers, Vol I, Basil Blackwell, Oxford, 1983, pp. 131 y ss.), en el sentido de considerar a la Lógica Deóntica como una lógica de satisfacción de normas, y definiéramos a una tautología deóntica como una norma cuya negación no puede ser satisfecha (op. cit., p. 141), la fórmula (Pp&Pq) É P (p&q) no lo sería, dado que su negación : Pp&Pq&Ph(p&q) podría ser satisfecha. En efecto, hay soluciones distintas para los casos: p&¬q = Pp; ¬p & q= Pq; p&q= Ph (p&q). (Con esto creo respoder a una objeción que me formulara Pablo Navarro respecto de esta parte del trabajo)

²¹ “Inconstitucionalidad y Derogación”, en Discusiones, año II, Nº 2, Bahía Blanca, Argentina, 2001, p. 11 y ss.

²² op. cit., p. 33.

²³ Ross, Alf, Sobre el Derecho y la Justicia, EUDEBA, Buenos Aires, 1963, p. 125.

²⁴ Alchourrón, Carlos y Bulygin, Eugenio, Introducción a la metodología de las ciencias jurídicas y sociales, Astrea, Bs. As., 1974, p. 150.

²⁵ En este trabajo me refiero como “solución”, a lo que Alchourrón y Bulygin entienden como “solución maximal” (Introducción.., p. 37)

²⁶ Orunesu, Rodríguez y Sucar, op. cit. p. 34. Aunque ellos llegan a la conclusión de no resultar clara la aplicación al caso del principio de minimización cuantitativa, porque no han tomado en cuenta que si se considera a N1 solo derogada en forma parcial, dicho principio impone esa derogación frente a la de N2.

²⁷ Dogmática Jurídica y sistematización del derecho, en Análisis Lógico y Derecho, cit.., p. 474. El ejemplo está utilizado para otros efectos. Tomaré solamente la parte que nos concierne.

²⁸ Serían casos incomparables, en la terminología de Alchourrón y Bulygin (Introducción, p. 148).

²⁹ Respecto de lex specialis, ver Guarinoni, Ricardo, op. cit.,p. 552.

³⁰ Guarinoni, R., Id. p. 550.

IR